-
Good source for ukulele chords -- Ukutabs.com
-
Piano Keys -- to help you transpose...

-
Easiest Keys on the Ukulele: C, G, Am, Em
-
Some songs in increasing complexity...
-
3 chords:
-
500 Miles (I'm gonna be)
-
Sunday Morning
-
Free-Fallin (beware fast chord changes),
-
She Will Be Loved,
-
Riptide
-
Folsom Prison Blues,
-
The Joker (one extra chord)
-
-
4 chords:
-
Hey Soul Sister
-
Mad World
-
Knockin on Heaven's Door,
-
I'm Yours,
-
Wagon Wheel,
-
Viva La Vida,
-
Have It All,
-
Yellow (Cold Play -- one extra chord at very end),
-
Happy Birthday,
-
Radioactive,
-
Smells Like Teen Spirit,
-
Somebody That I Used To Know
-
-
5 chords
-
All of me
-
Me and julio
-
Drops of Jupiter
-
Hello
-
Hallelujah
-
Wonderwall
-
Fireflies
-
Don't Stop Believin
-
Hey there delilah
-
-
6 chords
-
I will follow you into the dark
-
Piano Man
-
Country Roads
-
Better Together
-
Count on Me
-
-
More than 6 chords
-
You've got a friend in me
-
Dream a little dream
-
Let it go
-
In my life
-
La Vie En Rose
-
Yesterday
-
-
-
Songs on Dr. Uke's Site
-
Come Monday
-
Fire and Rain
-
50 Ways to leave your lover
-
Rainbow connection
-
Someone like you
-
Sweet baby james
-
The last day of physics! The test will be in Google Classroom, so check that out. Technically, the test is due tomorrow, because I'm not allowed to give a due date past tomorrow. But you can turn it in late if you want.
The test and the bonus problem are attached separately to the assignment.
If I don't see you at the Zoom meeting, have a great summer!
Mr. Stapleton
 Class
76
Wednesday, 5/27
Class
76
Wednesday, 5/27Warm-Up :
1. Identify any nodes and/or antinodes in this video of the "wave pool."
2. Which harmonic is this? Could there be other harmonics?
3. Two important wave-related terms are resonance and forced vibrations. What do the two terms mean, and how are they related? Which one applies to the body of an instrument? Which one applies to breaking glass with your voice? How about the Tacoma Narrows Bridge collapse?
-
Watch this one before the other one: Tacoma Narrows Bridge collapse -- Old footage
-
Watch the other one before this one: Tacoma Narrows Bridge collapse -- Discussion
The Plan -- Choose Your Own Adventure: Alas, our time has been cut short. Next Tuesday is now the last day on which an assignment can be made due. I had really hoped that we would have time to wrap things up with a test and a class project. Then I thought we could just do the project and that would be more fun and better for everyone. But now I realize that many of you would prefer the test. It would be less work, and it would probably be better for helping you to learn the core material. The best thing to do is to give you some choices. Here they are...
- Option 1 -- If you are making a string instrument, finish it up and record a song for me. Then email me a picture of the instrument and the song (it can be any song -- at least one verse). You get 100% for your final test grade!
- Option 2 -- Whether or not you are making an instrument, complete the Instrument Project. You will need some string instrument recordings to do this. You can join forces with a student who made an instrument; you can use your own instrument; or, if you want to do this project, but you don't have an instrument, email me and I will send you some recordings to use . The project grade will be your last test grade.
- Option 3 -- Complete the practice test today. I will assign the test on Monday, and it will be due on Tuesday.
No matter which choice you choose, you can fix it, retake it, turn it in late, etc. up to June 12th. By the way, the test will have a bonus problem, which you can solve for extra points on any of the three options -- but I anticipate it being difficult :-).
 Class
75
Wednesday, 5/20
Class
75
Wednesday, 5/20Warm-Up :
In this video of Chladni patterns, does the white substance (salt? powder?) settle at nodes or at antinodes? Why?
Today's Work:
- Notes:
- Practice Problems:
- Practice #1: 16.9 Practice Solutions I think these are pretty easy, so there's no video.
- Practice #2: Ch 16.10 and 17.5 practice Solutions. Video explaining solutions
Extra Stuff :
 Class
74
Monday, 5/18
Class
74
Monday, 5/18Warm-Up :
If you're standing next to a race track, what do you hear as the cars pass you?
a. Their pitch changes from high to low.
b. Their pitch changes from low to high.
c. There is no change in pitch.
Instrument Update -- Instrument construction playlist
Today's Work:
- If, since the time of ESS, you've forgotten the basics of how the Doppler Effect works, watch this short video.
- Complete
the Doppler Effect Practice
- Video explaining the formula and doing an example -- It's a weird formula, so watch the video. But don't go past 16:50.
- 17.4 Practice
- 17.4 solutions
Extra Stuff :
 Class
73
Wednesday, 5/13
Class
73
Wednesday, 5/13Warm-Up : The frequency of a wave describes number crests or troughs that pass a particular point in a given amount of time (a.k.a. cycles per second). The units are Hertz (Hz).
1. What is the approximate frequency of the waves on the right?
2. If the distance between two successive crests (i.e. wavelength) is 4m, what is the speed of the waves on the right?
3. What is the formula for wave speed, in terms of frequency and wavelength?
4. What's wrong with the cat's motion?
Today:
- Notes: Wave and Music theory relating to fret calculations Filled-in notes Notes Video By the way, I know that there's a simpler way to perform the fret calculations, but this way gives you the best practice with waves concepts. If you can figure out the simpler way, use it and give yourself a nice pat on the back. :-)
-
Practice: Modify this
fret calculation spreadsheet template
to create a spreadsheet that will calculate fret positions for any
length string
- Answers
for a 33cm bridge-to-nut distance @440Hz.
 This would be a 13" scale -- a little shorter than the smallest
instruments some of you will be making.
This would be a 13" scale -- a little shorter than the smallest
instruments some of you will be making. - Video showing how to set up the spreadsheet (This is an old one.)
- Answers
for a 33cm bridge-to-nut distance @440Hz.
________________________________________________________________
- Links etc.:
- General Wave Properties
- Excellent demos by Dr. Daniel Russell, at Penn State
- Ruffed Grouse Drumming -- no good unless you listen with headphones or speakers with good bass.
- Wave interference and standing waves
- General Wave Properties
- Standing wave simulation
- Make interfering and standing waves, using a shlinky
- Standing wave video
- Division of the octave
- Calculating vibrating string length (distance from nut to frets).
- Various Mechanical Waves Links
Warm-Up : No warm-up. Test today.
Today:
- Instrument Info:
-
Instrument top design; here's an example that's been turned in.
Yours can be a simple hand sketch on the template.

- If you aren't making an instrument, you will still have to do many of the activities. Some of those activities require an instrument, so you may need to find a partner who is making an instrument.
- Clarification -- instrument form, take 2. After you complete the design, fill out String Instrument Form, Take 2. Should I make that a separate assignment?
- I've already made the necks, so on the second form please choose the same neck length that you chose last time. If you can't remember which one you chose, select "can't remember"
- Due to concerns about tunability, if you chose a 19" scale length, I made one that's about 17" instead.
-
Instrument top design; here's an example that's been turned in.
Yours can be a simple hand sketch on the template.
- Questions about the test? I'm going to assign it right
after we're done with our video conference.
- Everybody has exactly the same version, but please don't cheat.
- Every box is worth 1 point.
- You do not need to include units.
Warm-Up : If we have time, discuss Class 69 warm-up.
Today:
- Test Review -- Circuits and Current
 Class
70
Monday. 5/4
Class
70
Monday. 5/4Warm-Up :
Imagine a 110V home circuit that powers two light bulbs, a 100W bulb and a 60W bulb.
1. Is the circuit most likely a parallel circuit or a series circuit? How do you know?
2. Which bulb will burn brighter when they are both turned on?
3. Through which bulb will more current flow?
4. Which bulb has a higher resistance?
5. Why do the bulbs use more power than the wires that carry current to the bulbs?
Today: Kirchoff's Rules
-- another tool for determining currents in circuits.- Handout: Kirchoff's Rules 21.3 Notes and practice
- Video of notes -- including problems 1 and 2
- All Solutions
Optional -- you may want to try this pHet simulation -- DC Circuit Construction Kit. You can use it to calculate currents and voltage drops in circuits (here's how).
 Class
69
Wednesday. 4/29
Class
69
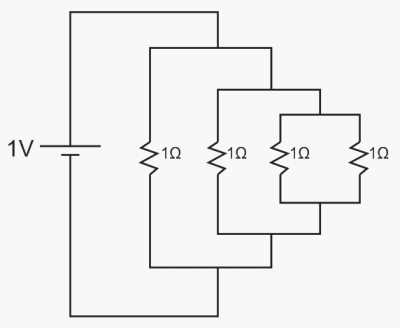
Wednesday. 4/29 Warm-Up :
Assuming that the wires on the right have zero resistance...
1. What is the equivalent resistance of the entire circuit?
2. How much current flows through the resistor on the far right?
3. Can you identify at least one easy way and one hard way to answer questions 1 and 2?
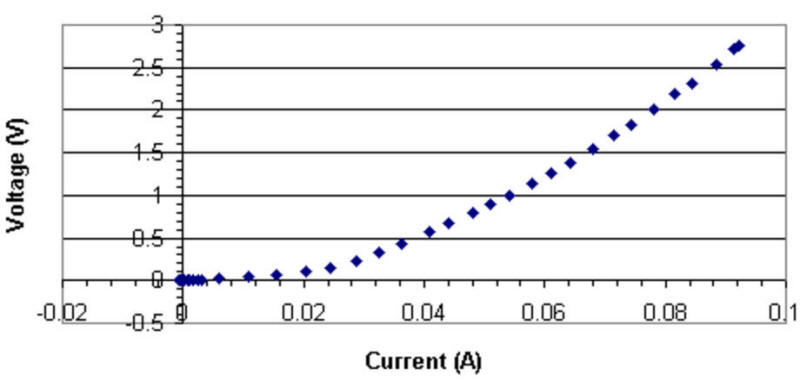 4. The graph below shows current flowing
through a light bulb at a variety of voltages. What does the slope
of this graph represent? Do these light bulbs obey Ohm's Law?
4. The graph below shows current flowing
through a light bulb at a variety of voltages. What does the slope
of this graph represent? Do these light bulbs obey Ohm's Law?
Today
: Chapter 20.4 is the section that I skipped over in the last class. After today, the only new material to learn in this unit is Kirchoff's Rules. We may do a little more practice- 20.4 -- Electric Power and Energy
- Practice -- 20.3, 20.4, 21.1:
- Equivalent Resistance Challenge (These are harder than the problems we have been working on recently. #2 is especially tricky.)
- Equivalent Resistance Challenge Solutions
- Video Explaining Solutions -- Equivalent Resistance Challenge
 Class
68
Monday 4/27
Class
68
Monday 4/27 Warm-Up :
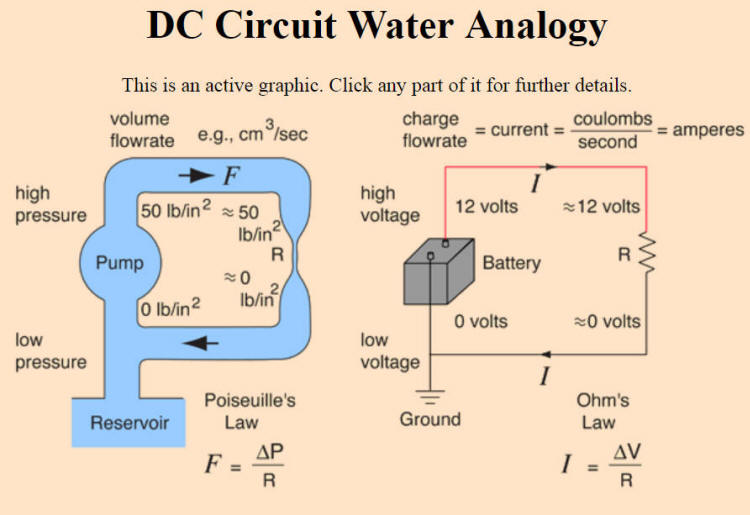
Check out the active graphic DC Circuit Water Analogy at Hyperphysics.com. According to the analogy...
1. Voltage is like _____
2. Resistance is like _____
3. Current is like _____
You should also check out this warning about how this analogy may cause some confusion for you in the future.
Today
: Normally, we do all of the notes below at one time. Given the circumstances, I am going to skip over parts of the notes in order to focus on resistance and calculating equivalent resistances in series and parallel circuits.- 20.3: Resistivity and Resistance, 21.1: Resistors in Series and Parallel. In the video, I am going over only 1-4.5, 11-15D, and 16A-D. I will return to the parts that I skip and fill them in later.
- Practice:
 Class
67
Wednesday 4/15 -- Last B day before break!
Class
67
Wednesday 4/15 -- Last B day before break!
Today
:- 20.1: Current
- 20.2: Ohm's Law
- 20.2 Notes and Practice (Ohm's Law) -- Blank Version
- 20.2 Filled-In Notes Notes Video
 Class
66
Monday 4/13 [Next class on Wednesday -- Then it's
the weekend! spring break!
(except for flex/homework/self-care Friday)]
Class
66
Monday 4/13 [Next class on Wednesday -- Then it's
the weekend! spring break!
(except for flex/homework/self-care Friday)]Warm-Up :
1. What can Tango and Cash teach us about electricity?
2. If you had to choose between touching a suspicous wire with the back of your hand or your palm, which should you choose? Why?
Today
:- Tests are graded and returned -- unless they were submitted after 7:45 on Sunday night.
- New Unit -- Current and Circuits
- Chapter 19.1 -- Electrical Potential Energy, Potential, and Voltage. Assignment due on Wednesday.
Warm-Up :
None
Today's Stuff
- Zoom Meet at 1:45
- Does anyone have questions about the practice test?
- Chapter 18 test is due on Thursday -- It's in Google Classroom
 Class
64
Friday-Monday 4/3 - 4/6, 2020
Class
64
Friday-Monday 4/3 - 4/6, 2020Warm-Up :
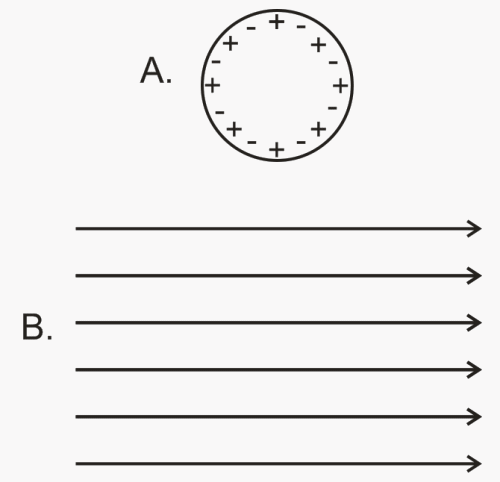
Suppose the neutral conductor in diagram A is placed in the electric field shown in diagram B.
1. How will the charges that are currently shown on the conductor rearrange themselves? Assume that both positive and negative charges can move equally well.
2. How will the electric field lines rearrange themselves?
3. Diagram C shows two conductors with excess positive charges.
Why do the excess charges reside on the conductors' surfaces?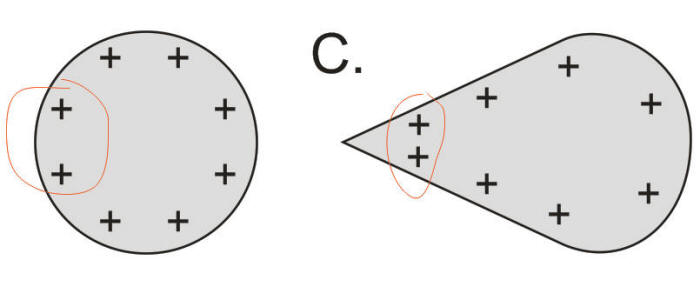 Why are the charges closer together near the pointy part of the
rightmost conductor? What implications does this have for Van de
Graaff generator design?
Why are the charges closer together near the pointy part of the
rightmost conductor? What implications does this have for Van de
Graaff generator design?
Today's Stuff
(See specific completetion requirements/assignments in Google Classroom):-
Warm-Up:
- Optional
-
Chapter 18 Practice Test 1:
 Class
63
Wednesday-Thursday 4/1 - 4/2, 2020
Class
63
Wednesday-Thursday 4/1 - 4/2, 2020Warm-Up :
How does a Van de Graaff Generator Work?
MIT video -- inducing dipoles with a VDG
If I have time, I'll provide my own, simplified, explanation of how VDGs work.
Today's Stuff
(See specific completetion requirements/assignments in Google Classroom):-
Warm-Up:
- Optional
-
Notes:
-
There are no notes for 18.8, but there are problems (below)
-
Practice :
______________________
In case you want to get ahead, here's what's coming next (I think)
-
Chapter 18 Practice Test 1:

 Class
62
Monday-Tuesday 3/30-3/31, 2020
Class
62
Monday-Tuesday 3/30-3/31, 2020
The website is back! I'm going to be doing a hybrid Google Classroom/Website system.
Warm-Up :
The electrophorus is charged by rubbing a cat(fur) against the top of an insulating plate (I). Then the conducting plate (C) is placed on top of the insulating plate and is touched by the physicist. Assuming that the cat fur has a strong affinity for negative charge...
1. What is the charge of the plate after it is touched by the scientist?
2. Explain how the conducting plate becomes charged.
3. What is the ground in this demonstration?
Givens for 2nd Retake (Test Version 3)
Today's Stuff (See specific completetion requirements/assignments in Google Classroom)
:-
Warm-Up: Charging and discharging an electrophorus
-
Watch the video by Heiko Timmers
-
Watch my video for further explanation of how the Electrophorus works
-
-
Notes:
-
Blank Notes: Notes 18.4 (Electric Field) -18.5 (Electric Field Lines).
-
-
Electric Field Hockey Phet Simulation and Questions:
-
You may not be able to open the simulation (because it's an old simulation; not HTML 5). If you can't open it on your computer, just watch the video (link below). Questions with link to simulation Answers to questions
-
-
Practice and Solutions:
I've moved into Google Classroom. Sort of sad. :-(
I've put today's stuff in Google Classroom. Please accept your invitation.
General Information
-
Google Meet today at 12:40. Here's the code: ftr-ddhv-nwm. This link should get you there, too.
-
Questions about the test problems
-
Other questions?
-
-
General Information
-
Google Meet today from 12:05-12:45. My tentative plan is to schedule video conferences that span what would be (if we were in school) the end of lunch and the beginning of 7/8, on A days. We'll see how that goes and adjust if necessary.
-
Tests are due today. I will grade the tests and provide videos explaining each of the problems. For this test there will be no partial credit. However, you only have to retake the numbers that you missed.
-
The retake is ready to go. I will share it with you, along with your unique values (link to values), later today. In most cases, the retake problems represent a reversal of the original test problems.
-
Here are links to the videos explaining the test problems. If I have graded your test, I have attempted to share them with you. Hopefully my sharing worked.
-
-
The next unit will be Electrostatics. I will be teaching the new unit through a series of videos that I will share with you.
Work to do:
-
Once I have graded your test, watch the video(s) that explain the problem(s) that you missed -- unless you didn't miss any. Try to solve any problems that you missed using my methods.
-
If you have watched the video segments for the problems that you have missed, and you still have questions, check in with me for a Google Meet session tomorrow at 12:40 PM. I'm not sure if this will work, but I have scheduled the meeting and copied this meeting ID: ftr-ddhv-nwm. If you want to attend, try opening Google Meet at 12:40 tomorrow and pasting that ID into the "join or start a meeting" box
 Hopefully, this will circumvent me needing to invite everyone.
Hopefully, this will circumvent me needing to invite everyone. -
Electrostatics Work -- Complete the green highlighted steps before class time on Thursday.
-
Here's a blank copy of the notes and practice. Printing them is not required. The notes cover two textbook sections. The practice is just for section 18.1 -- Notes and Practice -- 18.1 and 18.2 (Static Electricity & Charge, Conductors and Insulators)
-
Watch the 18.1-18.2 notes Video from last year's class -- I found it! Sorry for the "terrifying beeping."
-
In case you're interested, here's a link to the interesting V-Sauce episode that I mentioned at the very beginning of class (in the video from last year)
-
Complete the Chapter 18.1 practice problems. You don't have to turn them in. At some point I'll have you tell me whether you completed them. Here are the solutions...
-
After you finish the practice problems (or while you're finishing them), check your answers with these solutions. It might be a good idea to also watch my short screencast -- especially for the first couple of questions, which are conceptual.
-
In case you want a sneak preview of what last year's small test was like, here is Mr. Pennington's old test... Electrostatics Practice Test (Mr Pennington's Old Test) -- Answer Key
-
Today:
-
If you haven't done it already, watch this video of me giving an overview of the Rotational Motion Test. Some highlights...
-
You can retake individual problems
-
Notes are allowed; you can look up formulas (including moments of inertia).
-
My intention is to make this doable enough for everyone that there's no reason to cheat. At the same time, I think the format makes cheating more difficult; you can't just copy answers.
-
No partial credit, although wrong answers may be accepted if they represent correct calculations based on earlier wrong answers.
-
-
Complete this test and share it with me before class on Tuesday. You may use any class notes that you want, and you can look up formulas. You're just not allowed to get help from another human being (while you're taking the test). Share your test with me when you're ready for it to be graded or before class time on Monday, whichever comes first. At some point I may create a Google classroom, but I haven't done it yet.
-
Each of you will have unique values to use for every problem. You can find your personal values on this pdf. There were some mistakes on the first one. This is the revised version.
-
If you need them, here is a video with some clarifications relating to the specific problems on the test. I swear I turned my camera off, but apparently I didn't.
-
I'm going to invite everyone to a Google Meet session on Tuesday. I'll do it from 12:05-12:45, which, on wacky Tuesday schedule, would span the end of D-lunch and the beginning of 7/8. Participation will not be mandatory.
_____________________________________
12:06 - Here's the fixed screencast explaining the test. More to follow...
11:45 -- Please watch this screencast that I just uploaded explaining the test. Be aware that the givens that I will be providing in PDFs will be different than those you see in the video. This test is our first hurdle. Don't worry; there will be retakes. ***I just realized that some of your last names were visible in the video. I will replace the video with one that doesn't show your names. The link above is to my Google Drive, so hopefully that will limit other people's access until I get this replaced. I will be adding more information here in the next half hour or so. Mr. S.
11:28 Update... I'm going to make a screencast explaining the test format and upload it. I may have to upload a couple, because the dirty dogs at Google decreased the time limit to 5 minutes. At any rate, I will explain what we're going to do for the test. I'll share the screencast with you, leave a link here, and then add links (here) to everything else you need in order to get going on the test.
Mr. S.
Hi Physics 200 People! I was just in a hiring committee meeting, so I'm running a little behind. I wanted to have everything up here by the normal start of class, but I will probably be a few minutes late. It's 11:09 as I type this. If there's nothing more than this, check back in a half hour or so. Sorry for the delay!
Mr. S.
Warm Up: No warm-up today.
Today:
The highlight of today's class was this interesting (and fast) car! Click the photo to watch the video.
Check your email. I hope to start remote learning soon.
Mr. S.
Warm Up: No warm-up today.
Today:
Car project:
- Supplies and cars are concentrated in two locations -- the cart next to the filing cabinets (glue guns in the green bag) and under the island, on the side of the room near the sink. It's up to you to put everything back, because your physics mom had to stay home today.
- Turn-in Predicting Rubber Band Car Velocity and Acceleration Distance. If you're stuck on part of the calculations, just make up a value and use it to do your subsequent calculations.
- Make a video of your car crossing a floor tile and save the video for later confirmation (if necessary). Email me a calculation of your top speed. For simplicity, I will remove the distance error from scoring, so you don't have to measure acceleration distance. Your distance prediction will still be useful in helping you video your car at the right spot. To find your top speed, look for the moment when your rubber band releases from your car's axle (though if you no tension remains, the band may not release; your car may wind back up and stop itself).
- You can take your cars home if you want -- either to keep them or to continue working on yours.
Rotational motion test:
- Regarding our test, there will still be a test, but it won't be tomorrow. The possibility of cheating is a big issue, but I think I can come up with some incentives for not cheating (like not needing to) and some roadblocks to prevent cheating. I'll let you know when I know more, and I'll give you at least two full days notice before you have to take it. On the other hand, in an online context, the timing might be flexible. I'm tentatively planning on Thursday, but there may be some district ruling about when we can begin distance learning.
- Here's the Playlist from last class. I'm not sure if you can access it, but feel free to try.
Homework:
- Stay prepared for the test (notes and practice tests). Watch the videos if you need help.
- Finish anything that needs finishing
- Everything is homework, for now.
Warm Up: No warm-up today.
Today:
Coming Up:
- Monday: Car speed and distance measureent.
Homework:
- 4 minute drill Answers
- Review for the test (notes and practice tests). Watch the videos if you need help.
Warm Up:
1. Correction to 6d and 6f -- please record deceleration times.
2. What's the contingency plan for this class if school is closed?
3.
Good coronavirus article for teenagers.
Important Covid-19 graph
![]() .
FYI,
disease name vs virus name
.
FYI,
disease name vs virus name
Today:
- Continue working on:
Predicting Rubber Band Car Velocity and Acceleration Distance.
- If you can't remember how to determine the moment of inertia of a wheel/axle, review problem #6 in 19-20 Rubber Band Car Problem Set 1 Solutions
- Note -- you will be graded on the correctness of the calculations that you perform in the course of predicting your car's speed.
Coming Up:
- Friday: 4 minute drill. Questions about test? Finish car work. Turn in velocity and distance prediction sheets.
- Monday: Car speed and distance measurement.
Homework:
- Work on car calculations
- Review for the test (notes and practice tests). Watch the videos if you need help.
Warm Up:
1. Derive a formula that will allow you to find the velocity of your car if you know its kinetic energy
(and the wheel radii and moments of inertia).2. How do you predict the maximum kinetic energy of a rubber band car (in order to predict maximum speed)?
Today:
- If you're going to need a PC, log in.
- Check/review homework: problem section of Rotational Motion Practice Test # 2, Rotational Motion Solutions to Rotational Motion Practice Test #2.
- Continue working on:
Predicting Rubber Band Car Velocity and Acceleration Distance.
- If you can't remember how to determine the moment of inertia of a wheel/axle, review problem #6 in 19-20 Rubber Band Car Problem Set 1 Solutions
- Note -- you will be graded on the correctness of the calculations that you perform in the course of predicting your car's speed.
Coming Up:
- Thursday: 4 minute drill. Continue car work -- contest on Monday.
- Friday: Test
Homework:
- Review for the test (notes and practice tests). Watch the videos if you need help.
Warm Up:
1. From a physics standpoint, how does a car pop a wheelie?
2. How can a car be designed to minimize or maximize wheelies?
Today:
- If you're going to need a PC, log in.
- Check/review homework: Rotational Motion Practice Test # 2, Rotational Motion Solutions to Rotational Motion Practice Test #2.
- Continue working on:
Predicting Rubber Band Car Velocity and Acceleration Distance.
- If you can't remember how to determine the moment of inertia of a wheel/axle, review problem #6 in 19-20 Rubber Band Car Problem Set 1 Solutions
Coming Up:
- Wednesday: finish and turn in Predicting Rubber Band Car Velocity and Acceleration Distance and practice with your cars.
- Thursday: continue car work -- contest on Monday.
- Friday: Test
Homework:
- Complete the problem section of Rotational Motion Practice Test # 2, Rotational Motion Solutions to Rotational Motion Practice Test #2. If you don't understand the solutions, watch the videos below.
 Class
54
Tuesday, 3/10/20
Class
54
Tuesday, 3/10/20
Warm Up:
1. From a physics standpoint, how does a car pop a wheelie?
2. How can a car be designed to minimize or maximize wheelies?
Today:
- If you're going to need a PC, log in.
- Check/review homework: Rotational Motion Practice Test # 2, Rotational Motion Solutions to Rotational Motion Practice Test #2.
- Continue working on:
Predicting Rubber Band Car Velocity and Acceleration Distance.
- If you can't remember how to determine the moment of inertia of a wheel/axle, review problem #6 in 19-20 Rubber Band Car Problem Set 1 Solutions
Coming Up:
- Wednesday: finish and turn in Predicting Rubber Band Car Velocity and Acceleration Distance and practice with your cars.
- Thursday: continue car work -- contest on Monday.
- Friday: Test
Homework:
- Complete the problem section of Rotational Motion Practice Test # 2, Rotational Motion Solutions to Rotational Motion Practice Test #2. If you don't understand the solutions, watch the videos below.
 Class
54
Monday, 3/9/20
Class
54
Monday, 3/9/20
Warm Up:
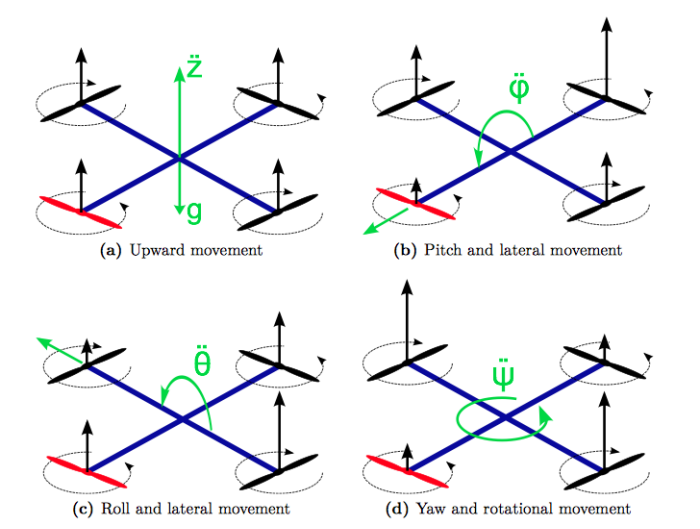
A quadcopter has four propellers that usually alternate in their directions of rotation.
- How does conservation of angular momentum enable this quadcopter to achieve a yaw?
- In order to pitch or roll, why can't one motor just speed up (without the opposite motor slowing down)?
Today:
- Log on to a PC.
- Get Rotational Motion Practice Test # 2, Rotational Motion
- Check/review homework -- problem section of Rotational Motion Test Review #1 Solutions to Pennington Test Review Problem solution video Multiple Choice Solution Video
- Work on
Predicting Rubber Band Car Velocity and Acceleration Distance --
- You can skip 2B, 3A, and 3B, and measure max friction force directly using a force meter.
- Build your optimal rubber band motor and create a table of force vs stretch distance (using a force meter).
- Measure the moments of inertia and frictional torques of both of your wheel/axle assemblies.
- Clean countertops, return tools and materials to their original locations
Coming Up:
- Tomorrow: finish Predicting Rubber Band Car Velocity and Acceleration Distance. Homework -- practice test #2 problems.
- Wednesday: turn in Predicting Rubber Band Car Velocity and Acceleration Distance and practice with your cars
- Thursday: more car practice
- Friday: Test, awards
Homework:
-
Complete the multiple choice section of
Rotational Motion Practice Test # 2, Rotational Motion
Solutions
to Rotational Motion Practice Test #2. If you don't understand the solutions,
watch the videos below.
Warm Up:
1. What kind of rear tires do dragsters use?
2. Why do drivers do a "burnout" before each race?
3. In what other ways do dragsters increase traction?

Popular Mechanics Dragster Info
Today:
- Check/review homework -- A5/6 -- Problems A7/8 -- Multiple Choice
- Work on Predicting Rubber Band Car Velocity and Acceleration Distance
Homework:
-
A7/8 Complete the problem section of Rotational Motion Test Review #1 Solutions to Pennington Test Review Problem solution video Multiple Choice Solution Video
-
A5/6 -- none
 Class
53
Thursday, 3/5/20
Class
53
Thursday, 3/5/20
Warm Up:
1. What is the function of the steel spheres in this bearing?
2. A bearing reduces friction, but it is not frictionless. What are the sources of friction in this bearing?
Fun Problems:
3. If the inner ring has an outer diameter of X, and the spheres have diameters of X/2, exactly how many revolutions do the spheres make for every rotation of the inner ring (assuming that the outer ring remains motionless)?
4. How many revolutions do the spheres make if the outer ring makes one rotation and the inner ring stays still?
5. What if each ring (outer and inner) makes 1 rotation, but in an opposite direction?
Today:
- Check/review multiple choice section of Rotational Motion Test Review #1 Solutions to Pennington Test Review
- Begin Predicting Rubber Band Car Velocity and Acceleration Distance
Homework:
-
A7/8 Complete the multiple choice section of Rotational Motion Test Review #1 Solutions to Pennington Test Review Problem solution video Multiple Choice Solution Video
-
A5/6 Complete the problem section of Rotational Motion Test Review #1 Solutions to Pennington Test Review Problem solution video Multiple Choice Solution Video
 Class
52.5
Wednesday, 3/4/20
Class
52.5
Wednesday, 3/4/20
Warm Up:
Suppose you need three squares of toilet paper, and one of your hands is unavailable.
1. What strategy might you use to tear off only three squares?
2. Why is this task easier with a nearly-full roll?
3. The custodians at Burlington High used to remove the rolls when they were almost empty, because it became nearly impossible to pull off more than one square at a time. Can you guess why?
Today:
- Check/review last week's homework: the rest of 19-20 Rubber Band Car Problem Set 1 SolutionsAssemble your cars.
- Begin Predicting Rubber Band Car Velocity and Acceleration Distance
Homework:
-
Complete the multiple choice section of Rotational Motion Test Review #1 Solutions to Pennington Test Review Problem solution video Multiple Choice Solution Video
 Class
52
Friday, 2/21/20
Class
52
Friday, 2/21/20
Warm Up: Rubber bands are not 100% efficient. If you do 2J of work in the process of stretching a rubber band, you won't get 2J of energy out of the rubber band when it snaps back. Suggest a simple way to estimate the efficiency of a rubber band.
Today:
- Updated Car Part Specifications spreadsheet.
- Steps for predicting your car's maximum velocity and acceleration distance
- Select and lay out your car parts on a virtual sheet of plywood.
Design some of your own, if you want.
- Open this link to the Rubber Band Car Part Buffet file.
- Save the file with your name in the file name. Make sure it's a .3dm file.
- Copy all of the parts that you want to the rectangle containing your chosen frame. Position them so that they don't touch. Save the file again.
- Email the file to jstapleton@ewsd.org. In the email, list the names of your group members.
Homework:
-
None
Warm Up: No Warm-up
Today:
- Test retake
Homework:
-
Finish the rest of 19-20 Rubber Band Car Problem Set 1 Solutions
-
Check out this spreadsheet with table of car part specifications. This should give you an idea of how much normal force will be pushing up against your wheels (and contributing to friction). Masses do not include hot glue, rubber bands, or string -- just wood, steel, and bearings.
-
Consider a frame length for your car, and decide on wheel size. Wheels can be scaled to any size you want, as long as they fit on the birch plywood (or as long as you make them from something that costs less than $1.)
 Class
51
Wednesday, 2/19/20
Class
51
Wednesday, 2/19/20
Warm Up: Falling cats continued...
1
. Can we simulate what this cat does on a lazy Susan?2. We have already agreed that you can't pick yourself up by your bootstraps. This video implies that you can turn yourself around boot straps (or maybe by a belt loop). Is this true?
Today:
- Check homeworks -- calculating I and Tfr Solution Checker (Stapleton access only). Turn in a small slip of paper with the following information in the following order:
-

- Review questions for the Momentum/Impulse Collision Test retake (conceptual practice questions -- Answers)
- Complete #1 and #3 of the lab measurements at the end of 19-20 Rubber Band Car Problem Set 1
Homework:
-
Due on Friday -- Finish the rest of 19-20 Rubber Band Car Problem Set 1 Solutions
-
Choose a frame length for your car, and decide on wheel size. Wheels can be scaled to any size you want, as long as they fit on the birch plywood (or as long as you make them from something that costs less than $1.)
-
Tomorrow -- test retakes and work time.
-
Friday -- lay out and submit your laser cutting car design in Rhino (CAD software).
 Class
50.5
Tuesday, 2/18/20
Class
50.5
Tuesday, 2/18/20
Warm Up:
- How do falling cats always manage to land on their feet?
- Why do falling people flail their arms around?
Today:
- Check/review homework: #1-2 in 19-20 Rubber Band Car Problem Set 1 Solutions
- Discuss why we're dropping parts h-j of #6.
- Finish wheel and axle data collection Solution Checker (Stapleton access only)
- Momentum/Impulse Collision Test retake conceptual practice questions
Homework:
-
Use your data to calculate the wheel and axle moment of inertia and friction from torque ( like #6, parts a-g)
-
Data you will need: falling mass, fall distance (similar to thread length), acceleration time, deceleration time, axle radius
-
 Class
50
Monday, 2/17/20
Class
50
Monday, 2/17/20
Warm Up: Suppose you need to want to build a camp fire. You have plenty of dry wood, but it's all big limbs that are too long to be manageable and too thick to break over your knee. Without using a saw or an axe, what's the best way to divide the wood into smaller pieces? Can you describe the proper technique? One solution.
Today:
- Check/review homework: problems #2-4 in 10.5 Angular Momentum Notes and Practice -- Notes Key -- Practice Key -- Solution to #1
- Start Rubber Band Car Project/Problems
- Get 19-20 Rubber Band Car Problem Set 1 Solutions
- Do #6 together
- Complete the Lab requirements at the back of 19-20 Rubber Band Car Problem Set 1
Homework: Complete #1-2 in 19-20 Rubber Band Car Problem Set 1 Solutions
 Class
49.5
Friday, 2/14/20
Class
49.5
Friday, 2/14/20
Warm Up:
Explain how this jar lid closure works, in terms of Torque
.You might also consider F=kx.
Today:
- Check/review homework
- 10.5 Angular Momentum Notes and Practice -- Notes Key -- Practice Key -- Solution to #1
-
We're essentially done with new rotational material. What
next? Options...
- Start working on rubber band cars next week. Finish the cars and the test after break.
- Review and wrap things up next week. Test on Friday before break. Maybe start cars next week. More rubber band car work after break.
Homework: Complete practice problems #2-4 in 10.5 Angular Momentum Notes and Practice -- Notes Key -- Practice Key -- Solution to #1
 Class
49
Wednesday, 2/13/20
Class
49
Wednesday, 2/13/20
Warm Up:
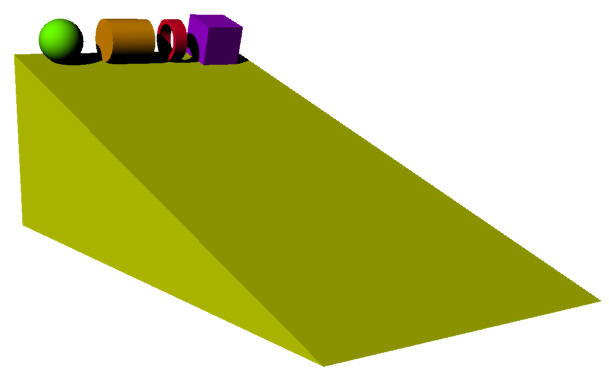
A sphere, a cylinder, a thin hoop, and a frictionless box are released from rest at the top of ramp. Their masses and heights are identical.
1. Rank the objects according to their arrival times at the bottom of the ramp.
2. Suppose the bottom end of the ramp is frictionless, and when they reach the bottom, the objects hit a vertical, frictionless wall. What motions, if any, would continue after impact?
3. How would the results be different if some objects had more mass or greater size than others?
4. How would the results be different if the ramp itself were frictionless?
Today:
-
Chapter 10.3-10.4
Notes and Practice: Dynamics of Rotation and Rotational Kinetic
Energy
Notes Key
- Dynamics of Rotation Practice Key
-
Kinetic Energy Practice Key
Homework: Finish all of the practice problems in Notes and Practice: Dynamics of Rotation and Rotational Kinetic Energy
- Dynamics of Rotation Practice Key
-
Kinetic Energy Practice Key
 Class
48.5
Wednesday, 2/12/20
Class
48.5
Wednesday, 2/12/20
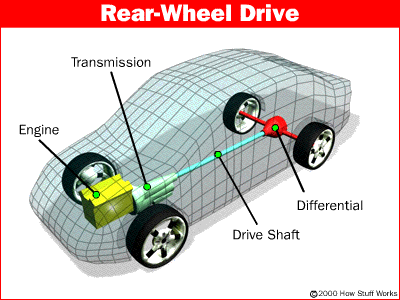
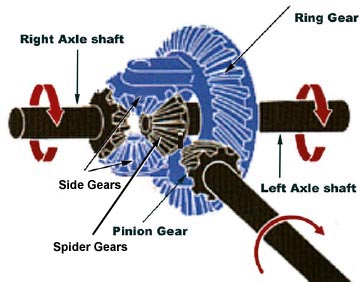
Warm Up:
1. What does a differential do?
2. How does a differential work?
Today:
-
Return tests -- retake day?
-
A7/8 -- Rotational Kinematics Notes
- Chapt 10.2 -- Kinematics of Rotation Notes -- Key
- Chapt 10.2 -- Kinematics of Rotation Practice -- Key
Homework:
-
A7/8 Kinematics of Rotation Practice -- Key
-
Rubber band car project planning -- think about your rubber band configuration, wheel size, and car length.

Warm Up: None
Today:
-
Small Test
-
Rotational Kinematics
- Chapt 10.2 -- Kinematics of Rotation Notes -- Key
- Chapt 10.2 -- Kinematics of Rotation Practice -- Key
Homework:
-
A5/6 Kinematics of Rotation Practice -- Key

 Class
47.5
Monday, 2/10/20
Class
47.5
Monday, 2/10/20
Warm Up:
1. Where does a compound bow store most of its energy?
2. What purpose(s) do the pulleys of a compound bow serve?
Today:
-
Check/review homework -- Angular Acceleration Practice -- Key
-
Questions about the test?
-
Rotational Kinematics
- Chapt 10.2 -- Kinematics of Rotation Notes -- Key
- Chapt 10.2 -- Kinematics of Rotation Practice -- Key
Homework:
-
Test tomorrow over all of the notes and assignments from this unit (Momentum/Impulse/Collisions). Part II of the test (problems) will be similar in structure to the practice test. Part I may be multiple choice, short answer, or both.
 Class
46.5
Thursday, 2/6/20
Class
46.5
Thursday, 2/6/20
Warm Up:
In the rotational (angular) motion unit, we will be using new units that are analogous to our current, linear units. You will need to be able to work in radians.
1. 360º = _____ radians
2. 90º = _____ radians
Today:
-
Return lab sheets
-
Questions about the test?
-
Angular Acceleration and Intro to Rotational Kinematics
Homework:
-
Test tomorrow over all of the notes and assignments from this unit (Momentum/Impulse/Collisions). Part II of the test (problems) will be similar in structure to the practice test. Part I may be multiple choice, short answer, or both.
-
Due on Monday -- Angular Acceleration Practice -- Key
 Class
46
Wednesday, 2/5/20
Class
46
Wednesday, 2/5/20
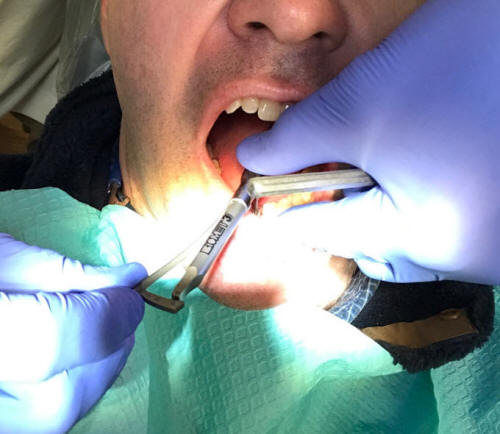
Warm Up:
1. Suppose you need to screw an abutment into a fixture that is implanted in someone's jaw. How can you make sure that you screw it in just tight enough, but not too tight?
2. What predictable effects (if any) does an increasing e have on collision time and collision force?
Today:
-
Check/review Lab activity -- Collisions, Impulse, Coefficients of Restitution. Answers
-
Torque
Homework:
-
Test on Friday over all of the notes and assignments from this unit (Momentum/Impulse/Collisions). Part II of the test (problems) will be similar in structure to the practice test. Part I may be multiple choice, short answer, or both.
Warm Up:
Suppose some hard objects collide with one another. Then the collision
is repeated, controlling all variables except that the collision is now cushioned.
1. In which case do the colliding objects experience a higher impulse?
a. When the collision is cushioned
b. When the collision is not cushioned
c. Can't tell
2. In which case do the colliding objects experience a higher maximum force?
a. When the collision is cushioned
b. When the collision is not cushioned
c. Can't tell
Today:
-
Questions about Mr. Pennington's Old Momentum Test. Answers/Solutions?
-
Finish and discuss Lab activity -- Collisions, Impulse, Coefficients of Restitution. Finish tomorrow.
-
Tomorrow -- start rotational motion unit-- Torque.
Homework:
-
Test on Friday over all of the notes and assignments from this unit (Momentum/Impulse/Collisions). Part II of the test (problems) will be similar in structure to the practice test. Part I may be multiple choice, short answer, or both.
 Class
45
Monday, 2/3/20
Class
45
Monday, 2/3/20
Warm Up: A low-friction physics cart is release from rest. It travels down a ramp, hits a spring, and bounces back up the hill before returning back down the hill again and continuing to bounce. If the cart travels 0.8m on its way down the ramp (0.8m = "closing distance") and 0.6m on its way back up the ramp (0.6m = "separation distance"), what is the coefficient of restitution (e) for this collision?
Today:
-
Check review homework: Linear Momentum Practice Quiz (2017-18 Test) Solutions
-
Lab activity -- Collisions, Impulse, Coefficients of Restitution. Finish tomorrow.
Homework:
-
Optional -- Mr. Pennington's Old Momentum Test. Answers/Solutions.
-
Test on Friday over all of the notes and assignments from this unit (Momentum/Impulse/Collisions). Part II of the test (problems) will be similar in structure to the practice test. Part I may be multiple choice, short answer, or both.
 Class
44.5
Friday, 1/31/20
Class
44.5
Friday, 1/31/20
Warm Up:
Renault Modus (compact car) vs. Volvo wagon in a head-on crash. (start at 4:30)
1. What happens?
2. Which is safer, a car that crumples in a crash or a car that is more rigid?
3. What questions remain after watching the video?
Today:
-
Check review homework: The rest of Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
Homework:
 Class
44
Thursday, 1/30/20
Class
44
Thursday, 1/30/20
Warm Up:
Suppose I stand a board on end and shoot it with a Nerf ® dart.
1. Am I more likely to knock the board over if I use a dart that sticks to the board or if I use a dart that bounces off of the board? Why?
2. Which experiences a greater impulse, the dart or the board? Or do they experience the same impulse?
Today:
-
Not everyone has turned in the ballistic pendulum spreadsheet
-
What barrel length will shoot a Nerf Dart fastest? How many pieces of cardboard will the dart penetrate?
-
Newton's cradle
-
Finish Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
Homework:
-
Finish the problems in Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
Warm Up:
1. Into which end of the "potato launcher" barrel should the projectile be placed before firing? Why?
2. What length barrel will give the projectile the greatest speed? [We have barrels up to 10 feet long. ]
3. Which new concept best explains the answer to #2 -- Conservation of Momentum or Impulse?
4. If we measure actual velocities of the projectiles, using photogates, and compare those to our predicted velocities, how do you think they will compare?
Today:
-
Finish Ballistic pendulum activity
-
Create a spreadsheet to calculate the velocity of a projectile based on: 1) projectile mass, 2) pendulum mass, 3) pendulum swing height, in meters
-
Check your spreadsheet using the launch 1 and launch 2 data in the notes relating to ballistic pendulums. Example
-
Create a projectile for the ballistic pendulum. Shoot it at the pendulum, and determine its velocity.
-
Measure actual velocity using photogates
-
Homework:
-
finish your spreadsheet. Share it with me when you're done.
 Class
43
Tuesday, 1/28/20
Class
43
Tuesday, 1/28/20
Warm Up: A steel ball, released from rest, rolls down a ramp in the classroom. Without using an electronic device, how might you determine the ball's speed at the end of the ramp?
Today:
-
Project form results -- controlling for unfair voting behavior
-
7/8 Check/review homework (6-12 in Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
-
Notes -- ballistic pendulums Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
-
Ballistic pendulum activity
-
Create a spreadsheet to calculate the velocity of a projectile based on: 1) projectile mass, 2) pendulum mass, 3) pendulum swing height, in meters
-
Check your spreadsheet using the launch 1 and launch 2 data in the notes relating to ballistic pendulums. Example
-
Create a projectile for the ballistic pendulum. Shoot it at the pendulum, and determine its velocity.
-
Homework:
-
finish your spreadsheet. Share it with me when you're done.
 Class
42.5
Monday, 1/27/20
Class
42.5
Monday, 1/27/20
Warm Up:
How can an understanding of momentum help you turn a towel into a better whip?
Today:
-
Fill out Project interest form
-
Check/review homework (1-12 or 1-5 in Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
-
Notes through elastic/inelastic collisions. Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
-
Snow lever status report
Homework:
-
None
 Class
42
Friday, 1/24/20
Class
42
Friday, 1/24/20
Warm Up:
1. What will happen if I hold a tennis ball on top of a basketball and drop them to the floor together?
2. What if I reverse their positions?
3. Why does this happen?
Today:
-
Return midterms -- check for grading errors, discuss answers
-
2nd Semester:
-
Momentum/Impulse/Collisions
-
Rotational Motion (Torque, Rotational Inertia, radians...) [rubber band cars?]
-
Electrostatics
-
Circuits and current
-
Electricity and magnetism? [electromagnets, motors, generators?]
-
Sound and waves [string instruments?]
-
Optics
-
-
Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
Homework:
-
A5/6 -- Complete #1-12 from Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
-
A7/8 -- Complete #1-5 from Notes and Problems: Momentum/Impulse/Collisions Notes key Problems Key
Review Packet Anwers to Review Packet -- 3rd try Last year's Midterm Study Guide
Warm Up:
Midterm discussion -- Questions? Remember that you can't leave early.
Today:
-
Optional -- test retake work time
-
Bungee Jump activity Activity directions and data sheet
-
If you don't finish the bungee activity today, you can finish later, and I can put the grade on next semester. It's more important that you focus on the midterm and/or your test retake. Instead of using a real egg in a wooden enclosure, I will have you use an equivalent mass.
-
Turn in 1 bungee sheet and one graph per group.
-
Award donuts and/or gluten-free snacks -- The current leaders are Eric et. al., with a distance of 15cm.
Homework:
-
Prepare for the midterm
Warm Up:
No warm-up today. Get started with the egg bungee activity.
Today:
-
Optional -- test retake work time
-
Bungee Jump activity Activity directions and data sheet
Homework:
-
Prepare for the midterm
-
Prepare for the bungee jump before the end of class tomorrow. Each group must turn in one activity and sheet and one graph.
Warm Up:
No warm-up today. Get started with the egg bungee activity.
Today:
- Return tests -- retake on Tuesday or Wednesday
-
Egg Bungee Jump Activity Activity directions and data sheet
Homework:
-
Test retake tomorrow or Wednesday.
-
If you need to finish your bungee drop tomorrow or on Wednesday, consult with your group members about test retakes.
 Class
39.5
Friday, 1/10/20
Class
39.5
Friday, 1/10/20
Warm Up:
You will be dropping an egg that will be stopped by a bungee. The force curves on the right represent force data collected from a variety of bungees.1
. Which bungee appears to behave like a spring with a constant k?2. What does the area under each curve represent?
3. If these data sets were used to calculate work done by stretching the bungee, which set(s) would cause an overestimate of work?
4. If we used the bungee that has a well-defined k, and we estimate how far a falling egg will stretch the bungee, are we more likely to underestimate or overestimate the actual distance? Why?
Today:
- Return tests -- retake on Tuesday or Wednesday
-
Egg Bungee Jump Activity
-
Finish first problem in Bungee practice problems. Solutions
-
Create a spreadsheet to streamline the process of solving one of these problems. Example Spreadsheet
-
Monday -- As a group of 2 or 3...
-
collect bungee force data and drop an egg. Contest details
-
Use some sample data to determine the fall distance of an example egg.
-
-
Homework:
-
Make a spreadsheet to use in the egg bungee drop.
-
Exam review
Warm Up: None
Today:
- Test -- Work and Energy
Homework:
-
Nothing required
-
Exam review
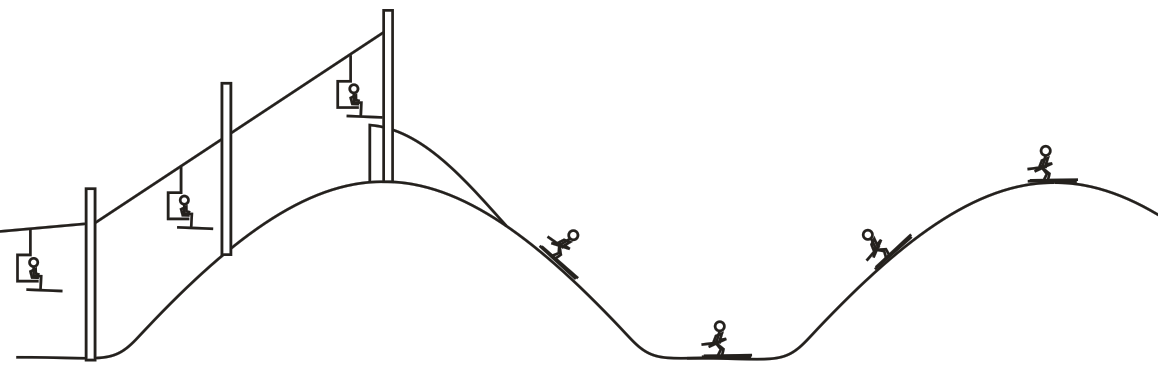
Warm Up:
1. When does each of these energy conservation equations apply to the diagram below?
2. Would your answer change if this were a completely frictionless environment?
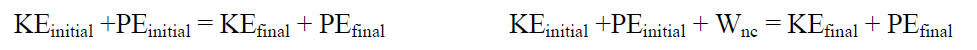
Today:
- Questions about tomorrow's test?
- Drill and practice
-
Egg Bungee Jump Activity
-
Continue Bungee practice problems. Solutions
-
Create a spreadsheet to streamline the process of solving one of these problems. Example Spreadsheet
-
Collect bungee force data.
-
Homework:
-
Test on Thursday
-
No other homework
 Class 38
Tuesday, 1/7/20
Class 38
Tuesday, 1/7/20
Warm Up: A spring hangs from the ceiling. When a mass m is attached to the end of the spring, released from that position, and allowed to come to rest, the end of the spring is a distance x lower than before the weight was added.
1. Which method below will not work for finding the spring constant k? Why?
Method 1: Set the weight of the hanging mass equal to the spring force; mg = kx. This gives us k = mg/x.
Method 2: Assume that the gravitational PE that is lost gets converted to spring PE, so mgh = 1/2 kx2 . Since the height lost is
equal to the stretch distance (x), we find that k = 2mg/x.
2. Sketch a graph of PE, KE, and OE versus time.
Today:
- Hand out (Midterm Review Packet) see changes to test details in class 39, below (green highlight).
-
Check/review homework:
-
Finish the problems in Pennington 2015-2016 test. Solutions
-
Complete the rest of the problems in Notes: Springs + Odds and Ends Notes key Problem solutions
-
-
Coming up:
7/8 Finish Notes: Springs + Odds and Ends
Egg Bungee Jump Activity
-
Create a spreadsheet to streamline the process of solving one of these problems. Example Spreadsheet
Homework:
-
Test on Thursday
-
No other homework
Warm Up:
1. A lightweight object and a very heavy object are sliding with equal speeds along a
level frictionless surface. They both slide up the same frictionless hill.
Which rises to a greater height?
A) The lightweight object, because it weighs less.
B) They both slide to the same height.
C) The heavy object, because it has greater kinetic energy.
D) Cannot be determined from the information given.
Today:
-
Check/review homework: Complete through Problem #4 in Pennington 2015-2016 test. #7 answer is incorrect Solutions
-
Coming up: Work/Energy Quiz on Thursday. Quiz retake next Tuesday or Wednesday.
?? Finish Notes: Springs + Odds and Ends Notes key Problem solutions
Homework:
-
Finish the problems in Pennington 2015-2016 test. Solutions
-
Complete the rest of the problems in Notes: Springs + Odds and Ends Notes key Problem solutions
 Warm Up:
Warm Up:
Sketch graphs of mechanical PE, KE, and OE (Other energy) versus time for...
1. Starting from rest, a child slides down a sledding hill of constant slope, reaching terminal velocity on the way. The bottom of the hill opens to a level meadow where the child comes to rest.
1b. Yesterday I gave you notes with this formula... KEi + PEi + Wnc = KEf + PEf + OEf What is the problem with this formula, as it
relates to the sliding child?
2. A dropped tennis ball bounces a few times before coming to rest.
3. A wad of soft clay flies horizontally toward a vertical wall. It hits the wall, falls a few meters to the floor, and comes to rest.
Today:
-
Check/review homework: Problems 1-3 in Notes: Springs + Odds and Ends Notes key Problem solutions
-
Coming up: Work/Energy Quiz next Tuesday, Quiz retake the following Monday or Tuesday.
-
Midterm Information (Complete Midterm Review Packet)
-
Topics/concepts will be the same as those tested by the unit tests. While the concepts, formulas, etc. will be the same as those tested on the unit tests, do not expect any of the questions or problems to be exactly the same as those on any unit test. As you study, make sure that you fully understand all of the concepts relating to the unit test questions and problems. Do not just memorize answers. To reduce your work time, some of the problems that included friction on the unit tests will not include friction on the midterm. Be prepared to solve problems without friction.
-
Format and Distribution of Material: 100 points total -- 25 Multiple choice (1 point each); 15 Problems (5 points each)
-
1-D Kinematics: 5MC, 3 Problems
-
2-D Kinematics: 6MC, 3 Problems
-
Newton's Laws (1-D): 6MC, 3 Problems
-
Newton's Laws (2-D): 1 Problem
-
Gravity and Circular Motion: 4MC, 3 Problems
-
Work and Energy: 4MC, 2 Problems
-
-
19-20 Semester 1 Formula list Extra points for opting out of the formula sheet (and G) -- 4%.
Down-sized tests representing topics covered on the exam
-
1-D Kinematics: MC and SA 1-16, Problems 2-5
-
2-D Kinematics: MC and SA 1-10, Problems 1, 3, 4
-
Newton's Laws (1-D) MC 1-9; SA 1, 3; Problems 1, 2, 3, 5
-
Newton's Laws (2-D) Problems 1, 2
-
Gravity and Circular Motion: MC 1-5, 7-12; Problems 1-5
-
Work and Energy (Pennington Test): MC 1-4, 7-16; Problems 1-3, 7
-
-
Finish Notes: Springs + Odds and Ends Notes key Problem solutions
Homework: Complete through Problem #4 in Pennington 2015-2016 test. #7 answer is incorrect Solutions

 Class 36.5
Thursday, 1/2/20
Class 36.5
Thursday, 1/2/20
Warm Up:
Sketch graphs of mechanical PE, KE, and OE (Other energy) versus time for a yo-yo that goes down and back up (without human assistance) until it runs out of energy. [What do the steel balls and springs do? What is the yo-yo's acceleration at the bottom?]Today:
Notes: Springs + Odds and Ends Notes key Problem solutions
Homework: Problems 1-3 in Notes: Springs + Odds and Ends Notes key Problem solutions
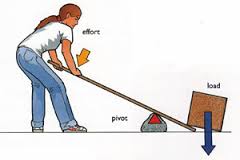


Warm Up:
he pictures on the right all show simple machines. Simple machines allow the same work to be done with more convenient combinations of force and distance.
1. Which "machine" is fundamentally different? Why?
2. Identify the task in each picture.
3. For each picture, identify the machine (s).
4. For each machine, tell how the machine alters the distance over which force must be applied by the human using the machine.
5. How does the machine alter the force that the human must apply?
Today:
-
Short Video: Santa Claus from an Engineer's Perspective
- Trucker's Hitch Song.
- Non-denominational fireplace with snappy logs
- Graded Assignment -- Learn to secure a load with a bowline and a Trucker's Hitch (slippery half hitch + slip knot), and explain how this arrangement allows you to tie a load with high tension.
- Video showing what to do and how to explain the mechanical advantage
- Bowline:
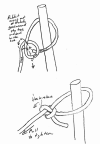 Slippery Half Hitch:
Slippery Half Hitch:
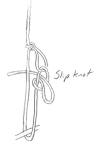
 Slip knot:
Slip knot:
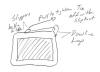
 How to secure a box with a Trucker's Hitch:
How to secure a box with a Trucker's Hitch:
Homework: If you didn't demonstrate mastery and understanding of the Trucker's Hitch, take a rope home and practice over break.
 Class
35.5 Thursday, 12/19/19
Class
35.5 Thursday, 12/19/19
Warm Up:
2. What would we have to do in order to change the orbit of a planet? (either move it away from the sun or toward the sun)
Today:
-
Return retakes
-
Check/return homework:
- Due Tomorrow-- Complete #6 in the "Work and Energy Practice Problems" in Work and Energy. Some answers/solutions Solutions to 3 and 4
- Due Tomorrow-- Complete the 2017 Work/Energy practice quiz Solutions
Tomorrow -- Machines, Trucker's Hitch, etc.
Homework: None
Warm Up:
None
Today:
-
Test Retake
-
Work time
-
Physics homework
-
Whatever you need to do
-
-
Tomorrow -- check/review homework. No new homework assigned.
-
Friday -- Machines, Trucker's Hitch, etc.
Reading (optional):
Homework:
- Due Tomorrow-- Complete #6 in the "Work and Energy Practice Problems" in Work and Energy. Some answers/solutions Solutions to 3 and 4
- Due Tomorrow-- Complete the 2017 Work/Energy practice quiz Solutions
 Class
34.5 Tuesday, 12/17/19
Class
34.5 Tuesday, 12/17/19
Warm Up:
1. Can you guess what the "sisyphus train" does?
2. How did it get that nickname?
3. In the context of physics energy problems, some forces are called conservative, and others are referred to as non-conservative. Can you guess the difference between the two?
Today:
-
Return rocket analyses -- if you want to submit it again, you can get half of the remaining points back. If you come in for help, I will make sure that you get the right answers this time.
-
Check/review homework: #1-5 of the "Work and Energy Practice Problems" in Work and Energy. Some answers/solutions Solutions to 3 and 4
-
Notes: PE and Law of Energy Conservation (handout:Work and Energy. Answers/solutions)
Reading (optional):
Homework:
- Retake tomorrow
- Due on Thursday -- Complete #6 in the "Work and Energy Practice Problems" in Work and Energy. Some answers/solutions Solutions to 3 and 4
- Due on Thursday -- Complete the 2017 Work/Energy practice quiz Solutions
- The homework load is pretty light. You may want to bring materials from another class to work on tomorrow -- if you're not retaking the test.
 Class
34 Monday, 12/16/19
Class
34 Monday, 12/16/19
Warm Up:
Do you know how to make a cloud in a 2-liter bottle, using water and a small amount of smoke? Can you explain it in terms of work and energy?
Today:
-
Turn-in fixed rocket analyses
-
New Unit -- Work and Energy:
Reading (optional):
Homework:
- Test retake on Wednesday
- Complete #1-5 of the "Work and Energy Practice Problems" in Work and Energy. Some answers/solutions Solutions to 3 and 4

 Class
33.5 Friday, 12/13/19
Class
33.5 Friday, 12/13/19
Warm Up:
1. How are g-forces dangerous to pilots?
2. In this video, a driver attempts to traverse a large loop-the-loop. In order to safely complete his mission, how many g's do you suppose the driver needs to tolerate?
Today:
-
Return tests
-
Turn in fixed rocket analyses if they're done. See homework note below.
-
Test retake next Wednesday.
-
New Unit -- Work and Energy:
Reading (optional):
Homework:
- I didn't have time to help people with the rocket analysis during Flex yesterday, so I told them they could turn it in on Monday. So... that option is open to everyone.
Warm Up: None.
Today:
-
Test
Reading (optional):
Homework:
- I didn't have time to help people with the rocket analysis during Flex today, so I told them they could turn it in on Monday. So... that option is open to everyone.
 Class
32.5 Wednesday, 12/11/19
Class
32.5 Wednesday, 12/11/19
Warm Up: The graphic on the right illustrates the possible scenarios for circle problems. Sketch or visualize a scenario based on each bullet point.
Today:
-
Check/review homework -- More practice-- Circular Motion, Gravitation, Kepler Solutions Solution to 16.2 --

-
Test review
-
Format -- 10-15 multiple choice over...
-
Centripetal motion
-
Law of Gravitation
-
Kepler's Laws (all 3)
-
-
7 problems -- solve for some variable in the related formulas.
- 3 Uniform Circle problems --
- see warm-up for possibilities
- Focus for vertical circles will be on top or bottom (not sides)
-
Law of Gravitation
-
Kepler's 3rd Law
-
Something relating to the formula for velocity of a satellite in circular orbit
-
Something relating to the formula for g.
- 3 Uniform Circle problems --
-
-
Reading (optional):
Homework:
- Study -- Test tomorrow.
 Class
32 Tuesday, 12/10/19
Class
32 Tuesday, 12/10/19
Warm Up:
1. What is a geosynchronous satellite?
2. What's the difference between a geosynchronous orbit and a geostationary orbit?
3. What is a space elevator?
4. In order to manually raise an elevator, would you have to apply a force greater than the elevator's weight? Explain.
Today:
-
Return test retakes
-
Check/review homework -- Gravity/Circles Practice Test -- 2018-19 Test -- Solutions to 18-19 Gravity/Circles Test
-
Work on the homework.
-
Test on Thursday; Rocket Analysis fixes due on Friday.
Reading (optional):
Homework:
-
More practice-- Circular Motion, Gravitation, Kepler
Solutions
Solution to 16.2 --

Warm Up: None
Today:
-
Test Retake
-
Work time
Reading (optional):
Homework:
- Due Tomorrow-- Gravity/Circles Practice Test -- 2018-19 Test -- Solutions to 18-19 Gravity/Circles Test (These are my solutions that I used to grade the tests; the solutions are not necessarily written so that they are easy to follow.)

 Class
31 Friday, 12/6/19
Class
31 Friday, 12/6/19
Warm Up:
From 2016-2017 EPS 200...
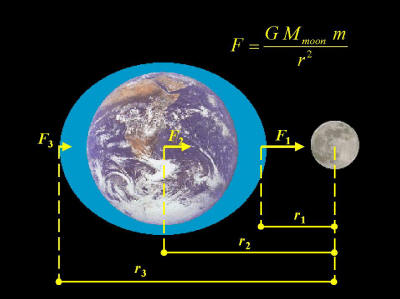
The Sun, Earth, and Moon are continually spaghettifying one another. On Earth, we see the effects of this spaghettification in the form of tides.
1. What causes spaghettification?
2. How much gravitational force do the Sun and Moon each exert on 1,000,000 pounds of water?
3. Even if there were no water on Earth, there would still be tides, just as there are tides on the Moon. Describe these tides.
4. Why do we always see the same side of the moon?
5. Is the Earth's 24 hour rotational period speeding up or slowing down over time? Answer
6. Describe two ways to feel gravity.
Today:
-
Check/review homework: #14 and 15 in Notes: Circles, Gravity, Kepler Solutions
-
Kepler's 3rd Law... orbital radius and period increase together, but which one increases faster?
-
Finish Elliptical Orbits Activity and discuss.
-
Get Gravity/Circles Practice Test -- 2018-19 Test -- Solutions to 18-19 Gravity/Circles Test (These are my solutions that I used to grade the tests; the solutions are not necessarily written so that they are easy to follow.)
Reading (optional):
Homework:
- Retakes on Monday Link to test answers (Newton's Laws in 2-D)
- Due on Tuesday -- Gravity/Circles Practice Test -- 2018-19 Test -- Solutions to 18-19 Gravity/Circles Test (These are my solutions that I used to grade the tests; the solutions are not necessarily written so that they are easy to follow.)
 Class
30.5 Thursday, 12/5/19
Class
30.5 Thursday, 12/5/19
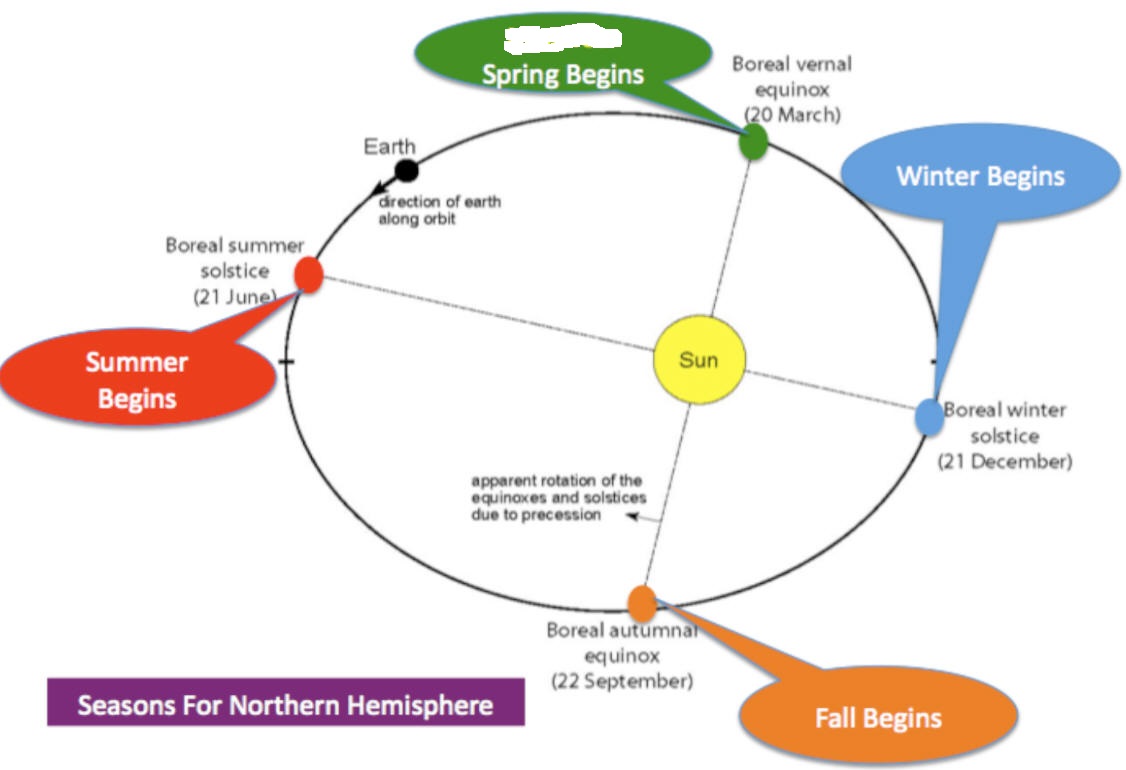
Warm Up: According to the diagram on the right...
1. At what approximate date is the Earth orbiting with the fastest speed? When is it orbiting the slowest?
2. Rank our seasons in order of length. Answer
Today:
-
Check/review homework: #8, 10, 12, and 13 in Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
-
Continue Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
Reading (optional):
Homework: .
- Complete #14 and 15 in Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
- Finish in class on Friday Elliptical Orbits Activity
- Retakes on Monday Link to test answers (Newton's Laws in 2-D)
 Class
30 Wednesday, 12/4/19
Class
30 Wednesday, 12/4/19
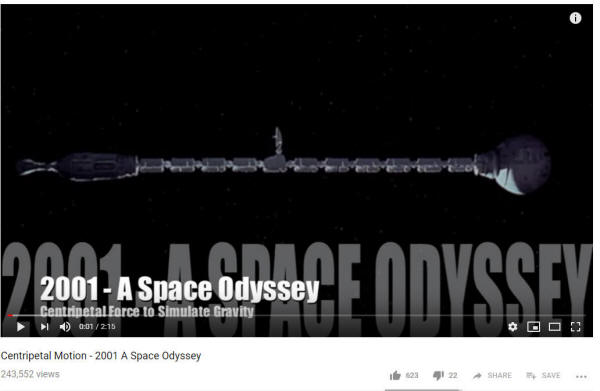
Warm Up:
1. Is this an answerable question -- Approximately how fast is the jogger in this video moving?
2. If the jogger turned around and jogged the other way, would he feel any different?
3. What must move in order for the person to experience simulated gravity... the space station, the person, neither, or both? What does "move" mean in outer space?
Today:
-
Check/review homework: Circular motion problems in Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
-
Continue Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
-
Law of Gravitation
-
Kepler's 1st and 2nd Laws
-
Reading (optional):
Homework: .
- Complete #8, 10, 12, and 13 in Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
- Due on Friday -- Finish Elliptical Orbits Activity
- Retakes on Monday Link to test answers (Newton's Laws in 2-D)
 Class
29.5 Tuesday, 12/3/19
Class
29.5 Tuesday, 12/3/19
Warm Up:
Consider a ball tied to the end of a massless string in the vacuum of space. The string is anchored at one end, and the ball is orbiting around the anchor point at a constant speed, held in its orbit by the string.
1. What forces are acting on the ball?
2. What forces are acting on the string?
3. How does this situation differ from the case of a real-world hammer throw (pictured on the right)?
Today:
-
Return Test
-
Chapter 6 (Circular Motion and Gravitation)
-
Brief look in online textbook -- Chapter 6.2 -- Centripetal Acceleration
-
Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
-
Reading (optional):
Homework: .
- Complete the "circular motion problems" (1-3), in Notes: Circles, Gravity, Kepler Solutions solution to #10 with 3rpm
- If you want to see the derivation of centripetal acceleration, see the online textbook.
 Class
29 Monday, 12/2/19
Class
29 Monday, 12/2/19
Warm Up:
Why does tension show up so often in physics problems? Is tension overrated?
Today:
-
Test
-
Return rocket analyses
Homework: .
- Rocket analysis corrections (optional). Due next Friday (12/13).
Warm Up:
We skipped it.
Today:
-
Return test retakes. Did anyone not retake the test -- and lose points on the short answer section of the original test?
-
Check/review homework: Practice Quiz over Newton's Laws in 2-D. Spreadsheet solutions to practice quiz
Homework: .
- Test on the Monday after break. Don't forget! I may send a reminder.
- Optional -- If you do this one, I suggest that you use the 0.2 friction coefficient on #4. If I remember correctly, the block won't actually move if the coefficient of friction is 0.4. Another practice quiz -- from three years ago. Video showing solutions
Warm Up: None
Today:
-
Test retake
-
Get practice test
Homework: .
- Practice Quiz over Newton's Laws in 2-D. Spreadsheet solutions to practice quiz
- Optional -- If you do this one, I suggest that you use the 0.2 friction coefficient on #4. If I remember correctly, the block won't actually move if the coefficient of friction is 0.4. Another practice quiz -- from three years ago. Video showing solutions
 Class
27.5 Wednesday, 11/20/19
Class
27.5 Wednesday, 11/20/19
Warm Up: Are astronauts and candles weightless when they are in the international space station? What word best sums up their motion?
Today:
- Check/review homework --Complete #2 and #4 in Masses Hanging and Dragged at Angles. Solutions to #1 and #2 solutions to #3 and #4
- Turn in Rocket Analysis.
- We will have a short test (over Newton's Laws in 2-D) on the Monday after break. You will get a practice test tomorrow, and we will go over it on Friday.
- If we have extra time, we will do a practice problem with a dangling mass.
Homework: .
-
Replacement Test Tomorrow.
-
Get practice test tomorrow -- Newton's Laws in 2-D
 Class
26.5 Monday, 11/18/19
Class
26.5 Monday, 11/18/19
Warm Up:
A waiter is delivering a chunk of bone, basted in synovial fluid, to some dinner guests. Touching only the serving tray (also made of bone), the waiter must deliver the dinner bone to the guests, and place it carefully on their table. Assuming the guests' table is to our left in the picture, describe what the waiter would need to do in order to make this happen? Can you sketch the forces on the bone?
Today:
- Work on Rocket Analysis.
Homework:
-
Rocket analyses are due on Tomorrow. Turn in one water rocket analysis for your group.
-
Replacement Test Day -- Next Thursday.
 Class
26 Friday, 11/15/19
Class
26 Friday, 11/15/19
Warm Up:
1. Cheryl wants to use some string and a nail to hang a treasured portrait of great-great-grandfather Ernesto as a young man. The portrait is rather heavy. Rank the three configurations on the right according to their risk of exceeding the breaking strength of the string.
2. How are static equilibrium and dynamic equilibrium different in physics problems?
Today:
- Return some papers
- Check/review homework -- Bodies on Inclines Answers (and some solutions ) to Bodies on Inclines video from A5/6 today
- Masses Hanging and Dragged at Angles Solutions to #1 and #2 solutions to #3 and #4 Video explaining #1 and #3.
- Work on
Rocket Analysis.
It's due on Monday. The grade will be based on correctness*,
but you will have a chance to fix your mistakes.
- Don't clear your data on #15.
- #11 is a complex problem.
- If you're looking for reasonable values to use in your free-body diagrams, check out the data and graphs provided by the water rocket simulation. Water rocket simulation link.
- To get a more accurate Cd,
change the spreadsheet time aloft formula, so that it looks like this...
 I was momentarily confused when I wrote the instructions for
that part of the spreadsheet.
I was momentarily confused when I wrote the instructions for
that part of the spreadsheet.
Homework:
-
Complete #2 and #4 in Masses Hanging and Dragged at Angles. Optionally, if you want more practice, do #1 and #3. Solutions to #1 and #2 solutions to #3 and #4 Video explaining #1 and #3.
-
Rocket analyses are due on Tuesday. Turn in one water rocket analysis for your group.
-
Replacement Test Day -- Next Thursday.
 Class
25.5 Thursday, 11/14/19
Class
25.5 Thursday, 11/14/19
Warm Up:
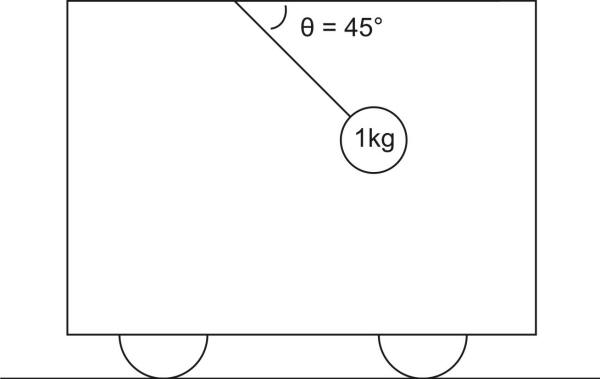
A 1kg mass is suspended by a string from the ceiling of a fully-enclosed train car. The angle shown remains constant.
1. Describe the motions of the mass and the train car in qualitative terms.
2. How can we find the tension in the string?
3. How can we describe the motions of the mass and the train car in quantitative terms.
Today:
- Bodies on Inclines Answers (and some solutions ) to Bodies on Inclines video from A5/6 today
- Work on
Rocket Analysis.
It's due on Monday. The grade will be based on correctness*,
but you will have a chance to fix your mistakes.
- Don't clear your data on #15.
- #11 is a complex problem.
- Water rocket simulation link.
-
Fix spreadsheet time aloft formula, so that it looks like this...

Homework:
-
Complete the problems in Bodies on Inclines Answers (and some solutions ) to Bodies on Inclines video from A5/6 today
-
Replacement Test Day -- Next Thursday.
 Class
25 Wednesday, 11/13/19
Class
25 Wednesday, 11/13/19
Warm Up:
1. One end of a rope is attached to the Gladys' belt. Gladys is pulling directly downward on the other end. Assuming that the pulley and rope are massless and fictionless, how much downward force must Gladys apply in order to ascend? Gladys weighs 500N.
2. This graph was created using a
pressure sensor launched in a rocket during A5/6.
 Why does the sensor think the rocket falls to a negative elevation at
the end of its flight?
Why does the sensor think the rocket falls to a negative elevation at
the end of its flight?
Today:
- A7/8 -- open up your video in Logger Pro.
- Return tests [score distribution
 .
Mean = 80.4%; Median = 82.6%]
.
Mean = 80.4%; Median = 82.6%] -
Fix spreadsheet time aloft formula, so that it looks like this...

-
Work on
Rocket Analysis.
It's due on Monday. The grade will be based on correctness*,
but you will have a chance to fix your mistakes.
- Don't clear your data on #15.
- #11 is a complex problem.
- Water rocket simulation link.
- Bodies on Inclines Answers (and some solutions ) to Bodies on Inclines Low resolution video from 2 years ago (first page of handout)
Homework:
Warm Up: None
Today:
- Test
Homework:
-
Optional -- Homerun Problem Replacement -- Find the foam ball labeled "FB." It should be on top of the stereo receiver in C209. Put it back when you are done measuing it. Assume that the ball's drag coefficient is 0.47. Suppose you want to launch this ball at a 60 degree angle, from the school roof (height = 4m) and have it travel a horizontal distance of 15m before hitting the ground (at a height of 0m). What initial speed must you give the ball have in order for this to work? For extra points, determine the speed required to make it travel a horizontal distance of 30m.
 Class
23.5 Friday, 11/8/19
Class
23.5 Friday, 11/8/19
Warm Up:
Suppose you're standing motionless on a motionless skateboard on level ground, and you want to travel (with the skateboard) in a direction parallel to the skateboard's length. If you are not allowed to touch anything except the skateboard...
1. Why is this a somewhat tricky task?
2. How can you accomplish the task?
3. Explain the physics behind why your method works.
Today:
- Check/discuss Newton's Laws Practice Test (Last year's test) Solutions Videos: Multiple choice, Short Answer, Problems 1-5, Problem 6
Homework:
Study for the test. What's on the test
-
Newton's Laws Practice Test (Last year's test) Solutions Videos: Multiple choice, Short Answer, Problems 1-5, Problem 6
-
Homerun Problem Replacement -- Find the foam ball labeled "FB." It should be on top of the stereo receiver in C209. Put it back when you are done measuing it. Assume that the ball's drag coefficient is 0.47. Suppose you want to launch this ball at a 60 degree angle, from the school roof (height = 4m) and have it travel a horizontal distance of 15m before hitting the ground (at a height of 0m). What initial speed must you give the ball have in order for this to work? For extra points, determine the speed required to make it travel a horizontal distance of 30m.
 Class
23 Thursday, 11/7/19
Class
23 Thursday, 11/7/19
Warm Up: If you need to stop a car quickly, why should you avoid locking the tires and skidding? What type of friction stops a car?
Today:
-
Return homerun problems. This is a required assignment. If you did not turn in an answer, or if you want a better score, you can solve the replacement problem, below.
-
Work on Rocket Analysis -- due on Wednesday. If you have a group of 4, split up into 2 groups of 2 for the calculations -- and turn in two separate sheets.
-
If you think you might have the longest time aloft, write your names, time aloft, video number, and donut preferences on the board.
-
Change of plans again -- we will have a test over Newton's Laws in 1-D. The test will be on Monday.
Homework:
-
Newton's Laws Practice Test (Last year's test) Solutions Videos: Multiple choice, Short Answer, Problems 1-5, Problem 6
-
Homerun Problem Replacement -- Find the foam ball labeled "FB." It should be on top of the stereo receiver in C209. Put it back when you are done measuing it. Assume that the ball's drag coefficient is 0.47. Suppose you want to launch this ball at a 60 degree angle, from the school roof (height = 4m) and have it travel a horizontal distance of 15m before hitting the ground (at a height of 0m). What initial speed must you give the ball have in order for this to work? For extra points, determine the speed required to make it travel a horizontal distance of 30m.
-
Warm Up:
Water rocket thrust = 2PA, where P = gauge pressure and A = nozzle cross-sectional area.100psi = 689,500pascals = 689,500N/m
22-Liter Bottle Neck diameter = 0.022m
Nozzle cross-sectional area (A) = pi*(0.022m/2)^2 = 3.8*10-4m2
Water Rocket Thrust = 2PA = 2 (689,500N/m2)(3.8*10-4m2) = 524N
Factoring a "Nozzle Loss Factor" of 0.16, thrust = 524N*0.84 = 440N

1. If thrust depends solely on pressure and nozzle diameter, why does the amount of water in the rocket matter? What is the optimal amount of water, and why is it the best?
2. If you check your car tire pressure, and the gauge reads 40psi, what is the actual pressure in the tire?
3. Why is rocket thrust 2PA, rather than PA? If you want a more complete explanation regarding why thrust =2PA, read this.
Today:
-
Insert your movie into Logger Pro.
-
Work on Rocket Analysis -- complete data collection steps. You can have class time for some of the calculations tomorrow. The entire analysis will be due on Monday.
Homework:
-
Homerun Problem Replacement -- Find the foam ball labeled "FB." It should be on top of the stereo receiver in C209. Put it back when you are done measuing it. Assume that the ball's drag coefficient is 0.47. Suppose you want to launch this ball at a 60 degree angle, from the school roof (height = 4m) and have it travel a horizontal distance of 30m before hitting the ground (at a height of 0m). What initial speed must you give the ball have in order for this to work?
-
Optional -- work on problem number 11, from the rocket analysis. This is a tricky problem. You will probably need more space for your work than the space provided in the analysis handout margins. Remember to change the number of bottles to 30.
 Class
22 Tuesday, 11/5/19
Class
22 Tuesday, 11/5/19
Warm Up:
1. How many 100 psi water bottles would it take to launch a human?
Today:
-
Check/discuss homeworks:
-
Home run problem
-
Work on Rocket Analysis
Homework: Optional -- work on problem number 11, from the rocket analysis.
Warm Up: None
Today:
-
Prepare rockets for launch.
-
Turn-in homework answers.
-
Launch rockets.
Homework: None
 Class
21.33 Thursday, 10/31/19
Class
21.33 Thursday, 10/31/19
Warm Up:
In the diagram on the right, the tension in the rope can be found by analyzing either mass. Rope tension = m1(g+a) = m2(g+a). How can this be true if m2>m1?
Today:
-
Check/discuss homework: Some more practice questions/ problems. Solutions
-
Announcement: due to the timing of things, we will be having one test over Newton's Laws (1-D and 2-D)
-
Enter your group's rocket pre-launch data into this form
-
Rocket launch on Monday -- split block. Tomorrow is too windy.
Homework: Use your completed trajectory spreadsheet to find the minimum speed and optimal angle for this most efficient home run...
What is the minimum speed at which a baseball must leave a bat in order to reach the fence (in the air) 340 feet away? What is the angle for this hit? Assume that the density of the air is 1.22kg/m3, the mass of the baseball is 0.145kg, the circumference of the ball is 0.23m, and the ball's drag coefficient is 0.45. You may also assume that the fence is short, with a height equal to the point of contact between the ball and the bat. Video help
Complete all of the following before class on Thursday.
-
Finish your projectile spreadsheet with drag. Spreadsheet Template: Projectile with drag Directions Video showing how to create the spreadsheet
-
Make a rocket.
-
Watch this video about rocket-making, starting at 7:34 (I've explained everything before that point).
-
Use this water rocket simulator to plan your dry mass and water volume. Remember that the pressure will be 100psi.
-
See other details below (class #19)
-
 Class
19.5 Friday,
10/25/19
Class
19.5 Friday,
10/25/19Warm Up:
1. How does NASA simulate weightlessness?
2. You are trying to transfer some drippy sauce across a dinner table using only a drippy spoon. The sauce needs to go from the pot to your plate without dripping. Touching only the spoon, how can you make this happen?
3. What would happen if you were standing on a bathroom scale in an elevator, and the elevator suddenly began to accelerate downward at 1g?
4. What is the source of the "butterflies in the stomach" when we fall?
Today:
-
Check/discuss homework
-
What's the plan for the next three class days?
Homework:
 Class
19 Thursday,
10/24/19
Class
19 Thursday,
10/24/19Warm Up:
1. This chicken weather vane is supposed to point into the wind. It points the wrong way. Describe two ways to fix it.
2. Why are hammers tricky to throw and catch?
Provide either the simple, superficial explanation or the complex explanation behind it. CM and Rotation3. A very light water rocket with no fins flies like a whiffle ball, but with less stablility. It can be improved by adding fins and some weights. Where should the fins and weights be added, and why?

Today:
-
Check/discuss homework: the rest of Practice Test: Newton's Laws in 1-D Answers but not solutions Problem Solutions
- FINISH Notes: 3rd Law, Tension Filled-in 3rd law notes
-
Discuss rocket construction
- Purpose: To investigate Newton's laws by measuring and modeling water rocket flight (including drag).
- Goal: Maximum time aloft for a controlled* flight. [Controlled means vertical flight with as little lateral movement as possible -- wind permitting. Aside from the turn-around at the zenith, there should be no rotation around any other axis than the long axis of the fuselage (i.e. fluttery flights will be disqualified).]
- Allowed materials: 1m duct tape, 2 2-liter bottles, weights (BYOW -- batteries, rocks, coins, sand...)
-
Limitations: sole power source = 100psi compressed air, expelling tap water; no ridiculously sharp components, such as nails protruding from the nose; bottle neck must be free from interference from fins,etc., so that the rocket can be attached to the launcher; rocket must be constructed with a consideration for recyclability.
-
Primary design and operational considerations: optimal mass, symmetry, minimal cross-sectional area, low drag coefficient, optimal water volume
-
Helpful website -- Water rocket simulator -- enter "100p" for pressure. Then maximize performance by trying different dry masses and water volumes.
-
Start this today -- Create a new projectile spreadsheet that acknowledges the existence of air (incorporates drag). We will be using this to analyze rockets and other projectiles flying through air.
-
Spreadsheet Template -- make your own copy, but don't change the data in the yellow cells. If you leave those data, you can use the screen shot below to see if your formulas are working.
-
Spreadsheet Directions -- I think there may be a mistake in here somewhere. There was one. Hopefully I fixed it.
-
For a screenshot of the working spreadsheet, click the thumbnail.
-
-
If you finish the spreadsheet, play with the water rocket simulator, above, to learn how to optimize
Homework:
-
 The
figure on the right shows Atwood's Machine.
Write equations for the acceleration of the masses
and the rope tension in terms of m1,
m2, and/or g.
You may also assume that the rope and the pulley are both massless and that there is no friction.
The
figure on the right shows Atwood's Machine.
Write equations for the acceleration of the masses
and the rope tension in terms of m1,
m2, and/or g.
You may also assume that the rope and the pulley are both massless and that there is no friction.
 Class
18.5 Wednesday,
10/23/19
Class
18.5 Wednesday,
10/23/19Warm Up:
1. Consider the 3kg mass. What does the magnitude of T2 need to be in order for the 3kg mass to accelerate upward?
2. Consider the 2kg mass. What relationship do T1 and T2 need to have in order for the 2kg mass to accelerate downward?
3. Consider the string between the 2kg and 3kg masses. What forces are acting on the string, and what conditions are necessary for the string to accelerate downward?
Today:
-
Return tests and other work.
-
Check/review homework
- The rest of Multibody Drill A (#2 and #4-6) Multibody Drill A Solutions -- Stapleton Tension Solutions to #5 and 6. Video for problem 2 Video for problem 6
- Conceptual #1-5 and Problems 1-6 from Practice Test: Newton's Laws in 1-D Answers but not solutions Problem Solutions
- Work on Notes: 3rd Law, Tension Filled-in 3rd law notes
Homework:
- Finish the rest of Practice Test: Newton's Laws in 1-D Answers but not solutions Problem Solutions
Warm Up:
None
Today:
-
Test retake
-
Work time
Homework:
- The rest of Multibody Drill A (#2 and #4-6) Multibody Drill A Solutions -- Stapleton Tension Solutions to #5 and 6. Video for problem 2 Video for problem 6
- Conceptual #1-5 and Problems 1-6 from Practice Test: Newton's Laws in 1-D Answers but not solutions Problem Solutions
 Class
17.5 Monday,
10/21/19
Class
17.5 Monday,
10/21/19Warm Up:
According to this article, emergency clinic records of 132 cats that jumped from windows of buildings showed a 90% survival rate. The average drop was 5.5 floors.
1. When does a falling cat experience zero net force?
2. When is a falling cat a "free-falling" cat?
3. When does a falling cat experience maximum net force?
Today:
-
Check/review homework -- #1 and 3 from Multibody Drill A Multibody Drill A Solutions -- Stapleton
-
Finish the practice problem in Multibody Drill A
-
Tomorrow -- retake and/or work time
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
- Ch 5.1: Friction
Homework:
- Chapter 3 (2-D Kinematics) Test retake tomorrow.
- Due on Wednesday (If you're not retaking the test, you can work
on this tomorrow, during class):
- The rest of Multibody Drill A (#2 and #4-6) Multibody Drill A Solutions -- Stapleton Tension Solutions to #5 and 6. Video for problem 2 Video for problem 6
- Conceptual #1-5 and Problems 1-6 from Practice Test: Newton's Laws in 1-D Answers but not solutions Problem Solutions
 Class
17 Tuesday,
10/15/19
Class
17 Tuesday,
10/15/19Warm Up:
Is it literally possible to "pull yourself up by your own bootstraps?" Explain.
Today:
-
Check/review homework -- The rest of Practice with forces in 1 dimension Answers/solutions
-
Do the practice problem in Multibody Drill A
-
It has been suggested that a tape measure can be used as a constant force for accelerating objects horizontally. In a group of 2 or 3, test this hypothesis, draw a conclusion, and provide evidence for your conclusion.
-
If you are retaking the recent test, you may be interested in these extra projectile problems. [solutions to extra projectile problems] They're similar to #3 and #5 on the original test.
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
- Ch 5.1: Friction
Homework:
- Complete #1 and 3 from Multibody Drill A Multibody Drill A Solutions -- Stapleton Video for problem 2 Video for problem 6
- Chapter 3 (2-D Kinematics) Test retake on Tuesday, 10/22
 Class
16.5 Monday,
10/14/19
Class
16.5 Monday,
10/14/19Warm Up:
1. If a Wiffle® Ball has a mass of about 45g, what is the upper limit of the amount of force a thrower can apply to a Wiffle Ball during the throw?
2. Why is there a limit to how much force can be applied to a thrown Wiffle Ball, no matter how strong the thrower is?
3. Describe the physical characteristics of the person who could apply the most force to the Whiffle Ball by throwing it. Who can throw a paper airplane the farthest?
Today:
-
Check/review homework -- Conceptual #3-10, Problems #1-13, 36, and 37 from Practice with forces in 1 dimension Answers/solutions
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
- Ch 5.1: Friction
Homework:
-
Complete the rest of
Practice with forces in 1 dimension
Answers/solutions
(not mine) Helpful formulas
--

- Chapter 3 (2-D Kinematics) Test retake on Tuesday, 10/22
 Class
16 Friday,
10/11/19
Class
16 Friday,
10/11/19Warm Up:
1. One way to find the center of mass (a.k.a. balance point) of a stick is to support it with two hands and then slowly move those two hands together until they meet under the stick's center of mass. Why does this method work?
 2.
Newton's 2nd Law says Fnet = ma. Why is it okay to use
this formula to calculate the force of gravity on an object that's
sitting still (i.e. not accelerating)?
2.
Newton's 2nd Law says Fnet = ma. Why is it okay to use
this formula to calculate the force of gravity on an object that's
sitting still (i.e. not accelerating)?
3. What would the scale read, in the diagram on the right?
Today:
-
New Unit: Newton's Laws?
-
Notes -- Friction. Filled-in notes.
-
One more test this quarter*, but it will go on next quarter, because we won't have time for a retake.
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
- Ch 5.1: Friction
Homework:
-
Conceptual #3-10, Problems #1-13, 36, and 37 from
Practice with forces in 1 dimension
Answers/solutions
(not mine) Helpful formulas
--
 Problem answers: 1. 75N, 2. 115kg, 4. 740N, 130N, 280N, 0N, 6.
-3600N 9. -780N 10. 13,000N 13. 50,080N, 44,300N
36. 103N, 0N 37. 0.98, 0.91.
Problem answers: 1. 75N, 2. 115kg, 4. 740N, 130N, 280N, 0N, 6.
-3600N 9. -780N 10. 13,000N 13. 50,080N, 44,300N
36. 103N, 0N 37. 0.98, 0.91. - The rest of Practice with forces in 1 dimension will be due on Tuesday.
- Chapter 3 (2-D Kinematics) Test retake on Tuesday, 10/22
Warm Up:
What if I put a large rock on my head, with a 2"x4" on top of the rock, and then I have someone hammer a large nail through the 2"x4"? Is this a good idea?
Today:
-
New Unit: Newton's Laws?
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
Homework:
- None :-(
Warm Up:
Test today
Warm Up:
It is possible to remove a sheet paper from under a dry erase pen without touching or tipping the pen. How can one do this without tipping the pen? Why does the pen usually fall?
Today:
-
Questions about the test? What's on the Chapter 3 Test
-
New Unit: Newton's Laws?
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
Homework:
- Study for the test. Go through all of the homework problems.
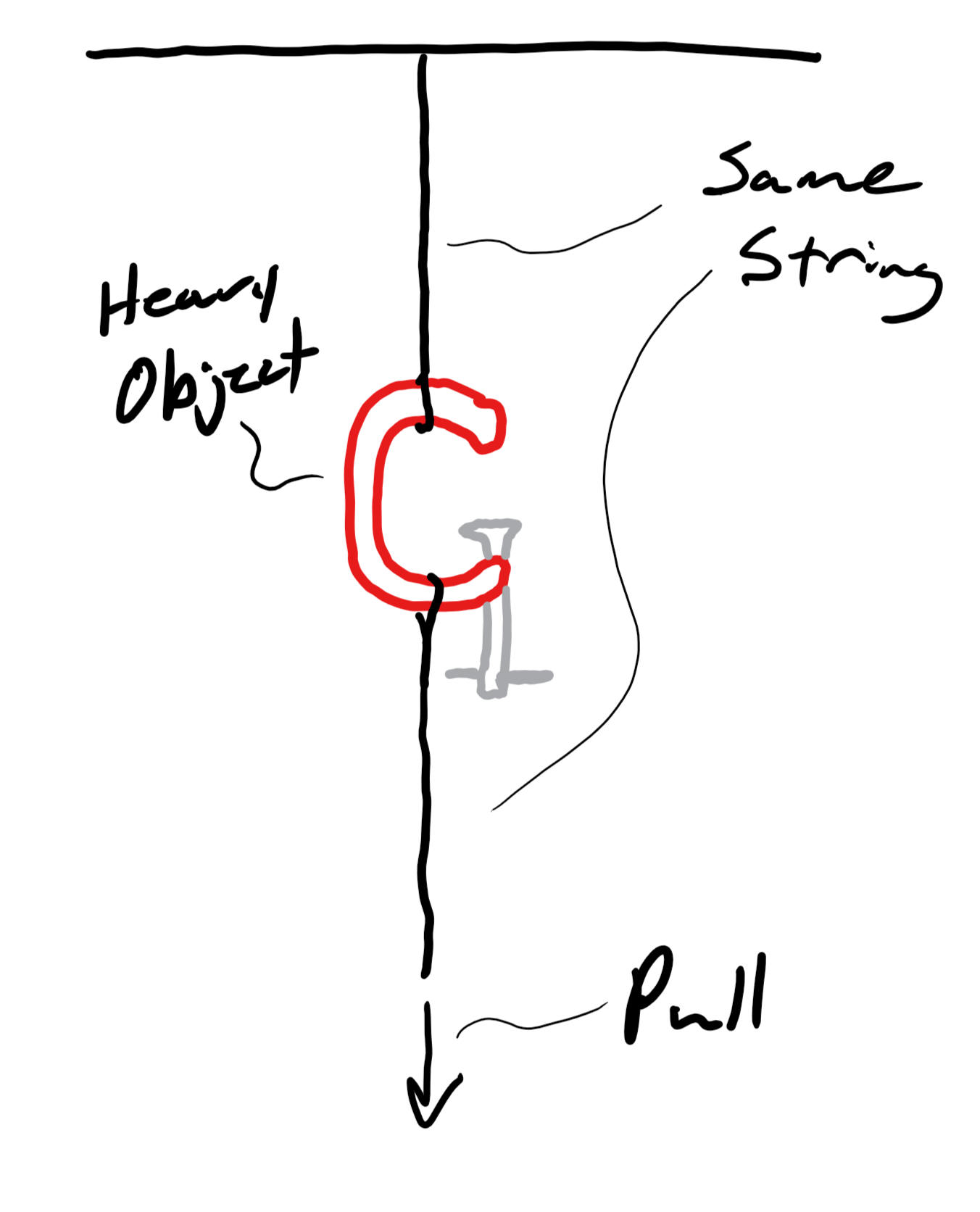 Class
14 Monday,
10/7/19
Class
14 Monday,
10/7/19Warm Up:
1. There is a heavy object suspended from the ceiling by a string. Another segment of the same string is hanging downward from the object. I am going to pull on the bottom string until one of the two strings breaks. Which string is going to break first? Why?
2. 1m/s = ____ mph. For Wednesday's test, memorize this or be able to calculate it based on a known conversion.
Today:
-
Check/review homework Chapter 3 Practice Test #2 Solutions Conceptual Questions Video Ch3 PTest Probs 1-2 Video Ch3 PTest Probs 3-4 Video
-
Another non-orthogonal River problem (video from class)
Online Textbook (OpenStax) Reading:
- Ch 4: Newton's Laws Intro
- Ch 4.1: Force
- Ch 4.2: Newton's 1st Law, Inertia
- Ch 4.3: Newton's 2nd Law, Concept of a System
Homework:
- Test on Wednesday. Review for the test. If you have any specific questions or topics that you would like to review, share them in class tomorrow.
- Check your email for two optional non-orthogonal river problems
Warm Up: What advice would you give next year's students, regarding preparation for this competition? Add suggestions to this Google Doc.

Today:
- Competition results
- Presentation of Donuts
- Return contest problems and project grades.
- Hand out homework
Homework:
Warm Up:
Projectile competition
Today:
Homework:
- None
Warm Up:
In the competition you will get two shots at each target. Suppose your first shot goes 40cm too far. How will determine the amount of launcher adjustment that is best for your next shot? my spreadsheet
Today:
-
Reminder -- class will be in C211 tomorrow (for the competition), not our usual C209 classroom.
-
Return launcher practice problems
-
At the end of class -- Go over the contest problems. Do not share these with the other class before the end of today.
-
No shooting is allowed after the handing out of the contest problems.
Homework:
- As a group, complete the projectile launcher contest problems. One calibration graph should be stapled to the sheet (velocity vs. launcher setting). This is a required grade. You can divide the work and fill out your sheet tomorrow. You will be using this during the contest and turning it in afterward.
- Make sure you have a plan for dealing with angled shots, making adjustments on your 2nd shot, etc.
 Class
12 Monday,
9/30/19
Class
12 Monday,
9/30/19Warm Up:
1. Due to the potential destructiveness of our new projectiles, the maximum contest muzzle velocity has been reduced to 8m/s. How can you use a horizontal launch from a stool to determine whether or not your launcher's muzzle velocity has reached this velocity?
2. Instead of calibrating with a horizontal launch, you might want to have one or two degrees of launch angle. Why?
3. Projectile contest problems may require shooting projectiles at any angle between horizontal and 70 degrees above horizontal. How can you precisely measure, control, and maintain the angle of your projectile launcher?
4. How can you customize your current spreadsheet to facilitate solving the launcher problems?
Today: Main focus for today, Wednesday, and Thursday: avoid damaging anything with steel balls!!!
- Turn-in/discuss launcher project practice problems.
- Videos for Mr. Pennington's chapter 3 test problems (plus a few requested multiple choice) are on my YouTube channel.
- Projectile Launcher Work:
- Never shoot a steel ball with a breakable object in your line of fire!
- Adjust launcher power -- we discussed how to do this in the warm-up.
- Create a calibration chart by launching horizontally from a
level or near-level surface.
- Use a cardboard backstop with noise-reducing paper towel.
- Record the launch height, horizontal displacement, and power setting for a range of velocities between 4m/s and 8m/s.
- Record the launch angle, if any.
- Create a calibration graph like this one. Manually fit a curve to your graph.
- Make plans for dealing with the complications arising from
angled shots...
- Launcher muzzle will be higher than the back of the muzzle, by a calculatable amount. To account for this precisely, you need to know the length of your launcher and the position of the hole.
- Using just your hands, it's hard to hold the launcher at a precise angle. You may want to devise a method or a device to deal with this difficulty.
- Set up your own test shots, and try them.
Coming Up:
- Today -- Projectile launcher work time and homework
- Wednesday -- Get the projectile contest problems. Final projectile launcher work time.
- Thursday -- Projectile contest. To give us more space, we will be switching rooms with Mr. Yando (C211).
Homework:
- Prepare for the projectile contest. Come up with a method of controlling launch angle. You may also want to improve your spreadsheet (video showing how).
 Class
11.5 Friday,
9/27/19
Class
11.5 Friday,
9/27/19Warm Up:
1.Does drag present a problem for our projectile launchers?
2. How can we answer this question?
Our spreadsheet Spreadsheet with drag
Today:
Coming Up:
- Friday -- review tonight's homework
- Monday -- Projectile launcher work time and homework
- Wednesday -- Final projectile launcher work time
- Thursday -- Projectile contest. To give us more space, we will be switching rooms with Mr. Yando (C211).
Homework:
- Use your spreadsheet to solve the launcher project practice problems.
Warm Up:
None -- test retake day
Today:
- Options: test retake, work on the homework, or both.
- If you're not retaking the test, and you want to work very quietly with other people on Mr. Pennington's test, sit at the lab tables.
Coming Up:
- Friday -- review tonight's homework
- Monday -- Projectile launcher work time and homework
- Wednesday -- Final projectile launcher work time
- Thursday -- Projectile contest. To give us more space, we will be switching rooms with Mr. Yando (C211).
Homework:
 Class
10.5 Wednesday,
9/25/19
Class
10.5 Wednesday,
9/25/19Warm Up:
1. Drawing from our growing arsenal of kinematics formulas, derive a specific formula for calculating the initial velocity (vo) of a projectile that is launched horizontally from a height (h) above the floor and which travels a horizontal distance x before landing on the floor.
2. Given the same initial velocity, how
will the range of a projectile launched at 80 degrees compare to the
range of a projectile launched at 10
 degrees?
(assume a symmetric flight path)
degrees?
(assume a symmetric flight path)
Today:
- Check/discuss #3 and #4 from Currents and Projectiles -- Notes and Practice Problems Filled-in notes and solutions Video of Notes from Class
- A8 -- anyone who wants to see the derivations in the part of the notes that we skipped can watch the video, above, and look at the filled-in notes (also above).
- Discuss retake -- For parts 1 and 2, each question or problem will have a similar counterpart (based on the same concept). Part 3 will be another extended problem, but each section will not necessarily have a specific counterpart on the first test. Please bring your first test and turn it in with your new test (so that I know how many points you originally recieved)
- If there's time, calibrate launchers.
Homework:
- None -- People who are retaking parts of the test tomorrow should study. And don't forget to bring your old test.

 Class
10 Tuesday,
9/24/19
Class
10 Tuesday,
9/24/19Warm Up:
1. Based on the diagram to the right, provide definitions for precision and accuracy. Which is easier to fix?
2. What does muzzle speed mean?
3. In our upcoming projectile contest, your launcher must be able to fire projectiles at muzzle speeds between 4m/s and 10m/s. If your launcher has a maximum muzzle speed of 11m/s, and your friend's has a maximum muzzle speed of 20m/s, whose launcher is more precise? Why?
4. Suppose you want to use your spreadsheet to find the muzzle velocity of a projectile launcher. What is the most precise method you can think of?
Today:
- Check/discuss #1 and #2 from Currents and Projectiles -- Notes and Practice Problems Filled-in notes and solutions Video of Notes from Class
- Solve the first of the launcher project practice problems.
- Begin preparing for the trajectory contest.
You will probably not get through all of this today. Calibrate your
projectile launcher so that you can launch your projectile at any
muzzle speed from 4m/s to 10m/s.
- Assemble your bands, string, and plunger. Sand your plunger, as necessary.
- Get a projectile and label it with your names.
- If you are working in the hall, and you need to measure launch angles with your phone, take one of the green passes.
- Test and adjust maximum muzzle velocity. Remember that the maximum contest velocity will be no higher than 10m/s.
- Develop a consistent protocol for firing, so that your shots are as precise as possible. Ideally, you should be able to hit exactly the same spot as long as you use the same release angle, release height, and release position.
- Create an accurate/precise table of muzzle velocity vs. release position. Later on, you will use these data to create a graph, and you will use that graph to shoot targets and avoid obstacles in the contest. Directions for optional photogate method. I'm not sure how many photogates we have.
- At the end of the block, remove your launcher's plunger and projectile, but leave the trigger attached to the launcher.
- Store your uniquely labeled projectile and your plunger assembly in the appropriate ziplock bag labeled for your class.
Homework:
- Complete problems #3 and #4 from Currents and Projectiles -- Notes and Practice Problems Filled-in notes and solutions Video of Notes from Class
Warm Up:
Use your spreadsheet to answer this question... Suppose you launch a projectile from the top of a tall building (80m above ground level), at an upward angle of 62 degrees and with an initial velocity of 40m/s. answers
1. How long will the projectile remain in the air before hitting the ground?
2. What maximum height will the projectile attain?
3. How far, horizontally, will the projectile travel?
Today:
- Discuss #5 from "Still More River Problems" simpler solutions to #5
- Notes: Currents and Projectiles -- Notes and Practice Problems Filled-in notes and solutions Video of Notes from Class
Homework:
- Complete problems #1 and #2 from Currents and Projectiles -- Notes and Practice Problems Filled-in notes and solutions Video of Notes from Class
 Class
9 Friday,
9/20/19
Class
9 Friday,
9/20/19Warm Up:
1. The pilot of a small plane is navigating by pointing her plane directly southward while maintaining an air speed of 100m/s. If the plane has an actual eastward velocity of 50m/s, sketch a velocity vector representing the air velocity.
To eliminate some calculations, you can describe the wind velocity by providing its two component vectors.
2. If there were no windshield, and the propeller were momentarily removed, would the pilot feel air blowing from straight ahead or from some other direction?
Today:
- Check/review homework: #2, 3,and 4, from "Still More River Problems" 2017 Solutions to Still more river problems -- with tables
- Currents and Projectiles -- Notes and Practice Problems Filled-in notes and solutions Video of Notes from Class
-
Create a projectile trajectory simulator (spreadsheet).
-
Here is a link to a Spreadsheet Template that you can use. Given an initial projectile speed and launch angle, your spreadsheet must:
-
Calculate the x and y position of your projectile at incrementally spaced moments during its flight.
-
Provide a graph of y displacement vs x displacement for the entire flight.
-
-
Use this screenshot to confirm that your spreadsheet works correctly. Enter the same values in yellow, and see if you get the same results. Your graph may vary depending on how many data points you include. You may want to add a trend line.

-
For videos showing how to create and fine tune the spreadsheet, see last year's videos on my YouTube channel.
-
Homework:
- Finish the spreadsheet described above.
 Class 8.5
Thursday,
9/18/19
Class 8.5
Thursday,
9/18/19Warm Up: Identify the component and resultant vectors for the following "river problems." Then sketch them using head-to-tail vector addition.
1. A boat travels eastward at a rate of 3m/s. The boat's heading is northeastward, and the boat's speed in still water is 8m/s. What is the velocity of the water in which the paddler is paddling?
2. A quadcopter has a velocity of 20m/s westward. The wind is blowing southward at a rate of 10m/s. What are the quadcopter's airspeed and heading?
3. The driver of a golf cart on an aircraft carrier uses a compass to head northward. The cart's speedometer reads 10mph. The aircraft carrier's heading is eastward, and it's speed in still water is15mph. The ocean current is northwestward at a rate of 5mph. What is the actual velocity (relative to the Earth) of the golf cart?
Today:
- Return and discuss tests
- Check/review homework: "Analytic Addition of Non-Orthogonal Vectors Drill" in the recent handout. Non-Orthogonal Vectors (Solutions). Watch my recent YouTube video if you need help.
Homework:
- #2, 3,and 4, from "Still More River Problems" 2017 Solutions to Still more river problems -- with tables
Warm Up:
No warm-up. Test day
Today:
- Test
Homework:
- Due on Thursday -- complete the rest of the "Analytic Addition of Non-Orthogonal Vectors Drill" in the recent handout. Non-Orthogonal Vectors (Solutions). Watch my recent YouTube video if you need help.
 Class
7.5 Tuesday,
9/17/19
Class
7.5 Tuesday,
9/17/19Warm Up:
Two canoe paddlers begin at the starting point in the diagram on the right. They paddle with a constant water speed. Paddler A keeps the canoe pointed westward while paddler B keeps the canoe pointed at the small island.
1. What do you think is the difference between water speed and speed?
2. Which paddler is following a heading?
3. Describe the shape of the path followed by each paddler.
4. Now suppose we increase the scale of the problem, and we remove the current. Paddler A again gets a compass, but only at the beginning of her journey. She points her canoe westward, begins traveling in that direction, and maintains her speed in a perfectly straight path (except for curving around the Earth). Assuming that her path is perfectly straight, why will she end up South of the island, regardless of her hemisphere?
Today:
- Check/review "Classic River Problem," from Combined handout with notes, analytic vector practice, and river problems
-
Questions relating to the test?
- For the practical problem, a timer and a meter stick will be provided. Make sure that you can measure in meters, using a meter stick.
- Test topics include all of the notes, homework, and practice tests before class #7. It wouldn't hurt to review some of the warm-ups, as well.
Homework:
- Due on Thursday -- complete the rest of the "Analytic Addition of Non-Orthogonal Vectors Drill" in the recent handout. Non-Orthogonal Vectors (Solutions). Watch my recent YouTube video if you need help.
Warm Up:
1. Suppose the two vectors on the right represent two forces acting on the clam. In what direction will the clam accelerate? What will be the magnitude of the net force accelerating the clam in that direction?
2. The diagram on the right shows a top view of a train car that is moving at a rate of 2m/s. You are in the car. In which direction and how fast should you walk in order to have the intended velocity shown on the right.
3. Sketch acceleration graphs for these events... my answers
a. A pitcher throws a fastball to a batter, and the batter hits a line drive that is caught by the pitcher. Sketch a graph of the ball's acceleration, assuming the pitch is moving forward.
b. A large, air-filled latex balloon is dropped from a height of 20 feet. The balloon hits a tile floor, bounces upward, and stops at some maximum height.
c. A pedestrian is walking to our right at a constant pace. As she does this, she swings her arms normally. Graph the horizontal acceleration of her right hand, beginning at the moment her left foot touches the ground and ending three steps later.
Today:
- Check/review #57 and #60 from "More Kinematics Problems". Solutions Any questions about 58 and 59?
- Discuss Test format: 48 points total
- New unit -- 2-D Kinematics
- Begin orthogonal vector practice.
- Combined handout with notes, analytic vector practice, and river problems (all three of the handouts below)
- Brief vector notes Answer Key
Homework:
- "Classic River Problem," from Combined handout with notes, analytic vector practice, and river problems
- Prepare for test on Wednesday. Come to class tomorrow with questions, if you have them.
Warm Up: List all of the kinematics formulas that we have been using
1. vave =
2. vave =
3. vfinal =
4. a =
5. displacement =
6. (vfinal)2 =
Today:
- Turn in optional 2 lap race problem
- Check/review Practice Test #2 Solutions except for conceptual #5 and problem #5 solutions to #5 and #5 Solution to hands-on problem
Homework:
- #57 and #60 from "More Kinematics Problems". Do the others if you want more practice. Solutions


 Class 6
Thursday,
9/12/19
Class 6
Thursday,
9/12/19Warm Up:
1. What kinematic information can we get by calculaing the area "under" the curve of a velocity vs. time graph?
2. What does the area under the curve of an acceleration vs. time graph tell us?
3. Does the area under the curve of a position graph tell us anything?
4. Suppose we graph the acceleration of a blowgun dart that is shot across the room, sticking to the opposite wall. How can #2, above, help us draw that graph?
Today:
- Finish reviewing homework -- Extended Kinematics Problems Answer Key
-
A7/8 --
Discuss sliding block solutions
My sliding
block video
My solution
- On a test, if you want partial credit, make sure you clearly write the original formula(s) that you are using.
- Questions about unit conversion practice?
- Practical Problem
- Use the materials provided in the room, to find the sphere's acceleration on each slope, and it's maximum speed. The sphere will probably fall off when you roll it, so here's a Link to a video that you can use to finish this.
Homework:
- Practice Test #2 Solutions except for conceptual #5 and problem #5 solutions to conceptual #5 and problem #5
- Replace a missing homework with 100% if you answer this correctly on your own and show your work... Suppose you run a two lap race. How much faster must your second lap be, compared to your first, if you want your average speed for the entire race to be twice the average speed of your first lap? Your answer can be in the form of a multiple (e.g. 2x faster, 3x faster, etc.)

 Class 5.5
Wednesday,
9/11/19
Class 5.5
Wednesday,
9/11/19Warm Up:
What would the graphs look like if you graphed acceleration for these events? My answers
1. A PE student runs from one end of the gym to the other and back (wall to wall) as fast as possible.
2. A basketball is dropped from high above a gym floor and bounces back up until its velocity reaches zero.
3. A skydiver steps out of a plane, begins to fall, opens a parachute, falls some more, and hits the ground. [Assume all motion is vertical.]
Today:
-
Discuss sliding block solutions
My sliding
block video
My solution
- On a test, if you want partial credit, make sure you clearly write the original formula(s) that you are using.
- Check/review homework -- Extended Kinematics Problems Answer Key
- Questions about unit conversion practice?
Homework: Finish the extended problems, if you haven't already finished them.
 Class
5 Tuesday,
9/10/19
Class
5 Tuesday,
9/10/19Warm Up:
1. A race car is traveling counterclockwise around a circular track. The car's speedometer stays on exactly 100mph the whole time.
Describe what happens to each of the following as the car makes one revolution around the track:
a) the car's speed b) the car's velocity c) the car's acceleration.
2. How would you use dimensional analysis to convert 4m/s to mph? Mathematically speaking, why does dimensional analysis work?
Today:
- Check/review homework --problem section of Mr. Pennington's Old 1-D Kinematics Test Answer Key.
- Turn in sliding block solutions and discuss.
- Note: there will be at least one problem requiring unit conversion on the test.
- The 1-D Kinematics Test will be next Wednesday (but we will probably be starting 2-D kinematics before that).
- Work on Extended Kinematics Problems Answer Key
Homework:
- Finish Extended Kinematics Problems Answer Key
- Optional homework in case you want unit conversions practice -- Unit Conversions Practice
Warm Up:
Match each position vs. time graph with the correct velocity and acceleration graph.
Today:
- Check/review homework. Discuss the acceleration graph. Why does it look terrible? What should it really look like? What's going on at different points in time? Stapleton graphs
-
Alone or in pairs (one group of three is allowed, per class), find
an answer to the sliding block question that follows...
- Theoretically, the coefficient of kinetic friction between
two surfaces allows us to calculate the force of friction
between two surfaces that are sliding past one another.
For an object freely sliding across a horizontal surface,
 .
Therefore, using Newton's 2nd Law, it can be shown that the
coefficient of friction = -a/g. Find the coefficient of
friction between a wooden block and the tile floor.
Briefly explain your methods and show your work.
.
Therefore, using Newton's 2nd Law, it can be shown that the
coefficient of friction = -a/g. Find the coefficient of
friction between a wooden block and the tile floor.
Briefly explain your methods and show your work.
- Theoretically, the coefficient of kinetic friction between
two surfaces allows us to calculate the force of friction
between two surfaces that are sliding past one another.
For an object freely sliding across a horizontal surface,
Homework:
- If necessary, finish the sliding block problem.
- Complete the problem section of Mr. Pennington's Old 1-D Kinematics Test Answer Key.
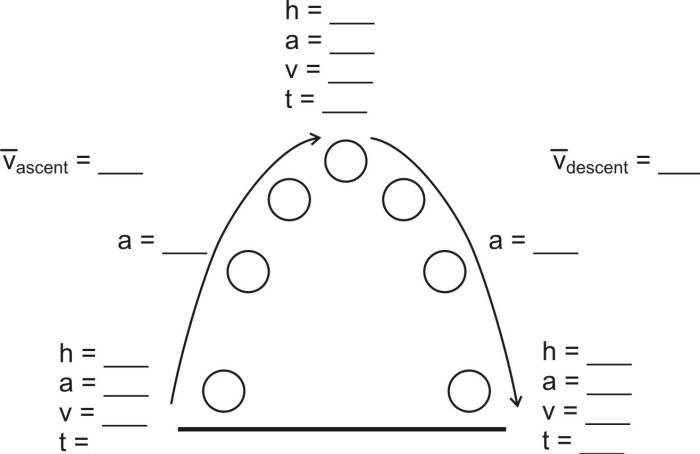 Class
4 Friday,
9/6/19
Class
4 Friday,
9/6/19Warm Up:
A ball is launched directly upward from the Earth's surface. The ball returns to Earth and hits the ground after a time of 10 seconds. Assuming no air resistance and g≈10m/s2, fill in the values in the diagram on the right. [Though the diagram appears to show horizontal motion, assume that there is none.]
Today:
- Presentation of donuts. Spool tractor contest results.
- Questions about Wednesday's homework? Answer Key -- Kinematics Formulas and Practice Problems
- Check/review Mr. Pennington's Old 1-D Kinematics Test Answer Key.
- Dr. W's class already disassembled the spool tractors, so we don't have to do it.
- Mr. Stapleton will demonstrate how to create a spreadsheet to produce motion graphs. It might be a good idea to take some notes.
Homework:
- Create Motion Graphs using Google
Sheets:
- Mr. Stapleton collected floor tile and video frame number data from this video. Use those data (in this Google Sheets template) to create graphs of position vs. time, velocity vs. time, and acceleration vs. time. You will need to make your own copy of the spreadsheet first. Rename it with your name.
- What to turn in:
- Print out the acceleration vs. time graph and add notes to the graph explaining what the spool tractor is doing at various times and how that relates to the points on the acceleration graph. For example, start with a note pointing to the positive dots at the beginning, and the fact that they indicate that the car is moving forward and speeding up.
- Propose an explanation for why the acceleration graph looks so bad [The answer is not that Mr. Stapleton was sloppy and careless!].
- Share the spreadsheet with jstapleton@ewsd.org.
- What to do if you're stuck -- Videos showing how to create the spreadsheet (I get better in each video) : Part 1, Part 2, Part 3
 Class
3.5 Thursday,
9/5/19
Class
3.5 Thursday,
9/5/19Warm Up:
The symbol "g" usually represents the absolute value of the acceleration of gravity near Earth's surface (in the absence of air resistance). The approximate value of g is 9.8m/s2, but the acceleration of objects due to gravity is -9.8m/s2.
For simplicity, use g = 10m/s2 to complete these motion graphs for an object with v0 = 20m/s and y0 = 0m.
[Ignore air resistance.]
Today:
- Check completion of homework -- quickly go over answers. If you have questions, watch one of these videos of me explaining the problems from last night's homework (#1-6, #7) If you still have questions, ask them tomorrow.
- Get your spool tractors tested, ASAP.
- Spool tractor prediction and selection form -- add your preferred Dunkin donut styles/flavors to the form.
Homework:
- Complete the multiple choice section of Mr. Pennington's Old 1-D Kinematics Test Answer Key.
 Class
3 Wednesday,
9/4/19
Class
3 Wednesday,
9/4/19Warm Up:
1. For letter a, on the right describe what an object could be doing in order to have both positive velocity and positive acceleration.
2. Do the same for the rest of the letters.
Today:
- Notes: Intro to Kinematics Formulas Answer Key -- Kinematics Formulas and Practice Problems
- Spool tractor challenge -- Try to be ready for contest measurements when we have 20 minutes remaining.
- Spool tractor prediction and selection form -- add your preferred donut styles to the form.
-



Homework:
- Finish the problems in Notes: Intro to Kinematics Formulas Answer Key -- Kinematics Formulas and Practice Problems
 Warm Up:
Warm Up:
1. Assuming that the man in the picture is 2m tall, and the frame rate of the camera was the usual 30 frames per second, what were the approximate maximum and minimum speeds of the object?
2. Based on your answers, do you think the assumption of 30 frames per second was too low, too high, or about right?
Today:
- Check/review homework -- Graph Comparisons Graph Comparisons solutions
- Turn-in signed course expectations
- Spool tractor challenge -- experiment, practice, and make notes today; contest tomorrow. Tomorrow, you will have at least 15 minutes to prepare before the contest.
-



Homework:
- None
 Class
2 Friday,
8/30/19
Class
2 Friday,
8/30/19Warm Up:
Use the velocity vs time graph on the right to sketch the shape of a corresponding position vs time graph.
[Hint: positive velocity corresponds to movement away from a motion sensor.]
Today:
- Get the free app, Coach My Video
- Turn-in signed course expectations
- Check/review homework
- Finish reviewing courses expectations.
- Complete Acceleration Notes -- Answer Key
- Spool tractor challenge -- try to build a spool tractor today; practice on Tuesday; contest on Wednesday.
-



Handouts:
Homework:
- Course expectations signatures.
- Complete Graph Comparisons Graph Comparisons solutions
.JPG) Class
1.5 Thursday,
8/29/19
Class
1.5 Thursday,
8/29/19Warm Up:
For each letter, describe what is happening to the person's speed and direction during the 10 seconds represented on the graph.
Today:
- Enter attendance
- Turn-in signed course expectations
- Check/review homework: motion matching questions
- 1-D Kinematics notes 1-D Kinematics notes Answer Key [*Note: we're easing in. Don't think it won't get harder.]
- Quickly run through course expectations?
- More sprotation -- why do the positions move one way and then the other?
\Online Textbook Reading:
Homework:
- Course expectations signatures.
- Suggested Reading (see above)
- Complete #5-8 in 1-D Kinematics notes 1-D Kinematics notes Answer Key
Physics 200: Mr. Stapleton
Warm Up:
 Spin
one of the "sprotating cylinders" by pressing one end until it squirts
out from under your finger. Try pressing the other end.
Spin
one of the "sprotating cylinders" by pressing one end until it squirts
out from under your finger. Try pressing the other end.
When the cylinder is spinning, why do you only see the symbol that you press?
Today:
- ___ students log in to desktops ASAP
- Learn names/pronunciations
- Enter attendance
- Student info sheet
- Check to see if you're on my email list, find my website, and see if your chromebook is working in here.
- Preview
- of the year (see last year's site).
- This unit -- check out the practice tests from last year's class 6.
- Briefly go over course expectations (grading, homework, talking, clean-up)
- About Me (mostly)
- Motion Matching Activity
- Directions: Matching Motion Graphs with motion detector (Web page)
- Answer questions at the end of the velocity notes
- ***A5/6 has D lunch (12:40) --
- B-Day Split block times (I think) are:
- B5 -- 1150-12:28
- B6 -- 12:32-1:10
Handouts:
Online Textbook Reading:
Homework:
- Finish the motion matching questions at the end of 1-D Kinematics notes 1-D Kinematics notes Answer Key
- Get your course expectations signed and then return them.
- Suggested Reading (see above)