 Class
41: Friday,
1/10/25
Class
41: Friday,
1/10/25Warm Up:
In this video, a driver supposedly enters a loop-the-loop at a speed of 36mph (16.1m/s). The driver supposedly experiences 6g at the bottom and approximately 0g at the top. They say the loop is 40feet high, so the radius is approximately 6.1m.
1. Calculate the values of g experienced by the driver at the bottom and the top.
2. Why don't your calculations match theirs?
Today: Review for the midterm
- Questions?
- Midterm Exam Topics (PDF)
- Jeopardy:
Homework: prepare for the :midterm
 Class
40.5 Thursday,
1/9/25
Class
40.5 Thursday,
1/9/25Warm Up:
1. How much does a 100 pound person weigh on the ISS (International Space Station)? Explain.
a. 0 pounds b. 89 pounds c. 100 pounds d. 111 pounds
2. Would a candle "work" on the ISS?
Today:
- Some more river problems (all 4 of the types that might appear on the exam)
-
Midterm
- Question -- if there is a 2D Forces problem on the midterm, how would you like it to be graded? The final answer, multiple steps, or optional partial credit for multiple steps
- Midterm review -- no one has emailed me a request for practice problems
Homework: prepare for the midterm

Warm Up: What do all of these things have in common?
Today:
- Test retake
-
Midterm
- Question -- if there is a 2D Forces problem on the midterm, how would you like it to be graded? The final answer, multiple steps, or optional partial credit for multiple steps
- Midterm review -- no one has emailed me a request for practice problems
Homework:
- Prepare for the midterm
 Class
39: Tuesday,
1/7/25
Class
39: Tuesday,
1/7/25Warm Up:
1. What would happen if you made a hole through the center of the Earth, and you jumped in? Spreadsheet calculations2. If you made it all of the way through, where would you come out? (antipodes map)
3. What's the orbital period of a low orbit satellite? Assume, for the purpose of calculations, that the satellite orbits just above Earth's surface (with no air resistance).
Earth's radius = 6.38x106 m. G = 6.67x10-11Nm2/kg2. Earth Mass = 5.97x1024kg
Today:
- Midterm review
- Update on bonus points for memorizing the midterm formulas
Homework:
- Optional retake tomorrow.
- Prepare for the midterm
 Class
38.5: Monday,
1/6/25
Class
38.5: Monday,
1/6/25Warm Up:
1. Can you guess what the "sisyphus train" does?
Today:
- Check/review homework.
- Go through the old tests. Links are here in Google Classroom Stream
- Test retake on Wednesday
- Some review options:
Homework:
- Review the old tests. Come to class with requests for specific types of practice.
 Class
38.5: Friday,
1/3/25
Class
38.5: Friday,
1/3/25Warm Up: How do you remove the coin from the YOT?
Today:
- Check/review Phases 1 and 2
- Course Recommendation Surveys
- Work time -- Phase 3 of review problem
-
If you want more practice materials, here are the unit handouts and
solutions. There is a practice test at the end of every handout.
Midterm problems will be similar to past practice test and test
problems. Questions will be similar to past test questions. I
would recommend trying problems and questions from the PDF before
you look at the answer key.
- Motion in 1 dimension: Unit 1 Handout (PDF) Unit 1 Answer Key
- Motion in 2 dimensions (river problems and projectile motion): Unit 2 Handout (PDF) Unit 2 Answer Key
- Forces in 1 dimension: Unit 3 Handout (PDF) Unit 3 Answer Key
- Forces in 2 dimensions: Unit 4 Handout (PDF) Answer Key
- Circular Motion and Gravity: Unit 5 Handout (PDF) Answer Key
Homework:
- Phase 3 of Review Problem 1 (PDF) -- Solutions
 Class
38: Thursday,
1/2/25
Class
38: Thursday,
1/2/25Warm Up: What's happening to this guy? Why? How does it work?
Today:
- Midterm review handouts:
- Optional Gravity/Circles Test Retake next Wednesday.
Homework:
- Phases 1 and 2 of Review Problem 1 (PDF) -- Solutions
Warm Up: Some cultures celebrate a character called Santa Claus, who delivers presents around the world in a sleigh. This event occurs over a time interval known as Christmas Eve. Starting from rest, if Santa were to deliver a present to every child who believes in him, how fast would Santa need to accelerate between stops in order to deliver all of the presents on Christmas Eve? Santa Claus from an Engineer's Perspective
Today:
- Cozy, crackling fireplace
- Return Tests
- Discuss AP
-
Learn to secure a load with a bowline and a Trucker's Hitch
(slippery half hitch + slip knot), and explain how this arrangement
allows you to tie a load with high tension.
- Here's a video showing exactly what to do.
- Bowline:
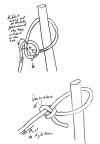 Slippery Half Hitch:
Slippery Half Hitch:
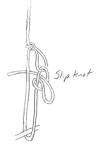
 Slip knot:
Slip knot:
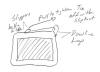
 How to secure a box with a Trucker's Hitch:
How to secure a box with a Trucker's Hitch:
- **If you can still demonstrate this when we take the energy test, you can earn 2% bonus points on the test -- and you'll have an very useful skill!
Homework:
- None
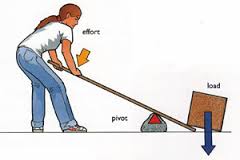


Warm Up:
The pictures on the right all show simple machines. Simple machines allow the same work to be done with more convenient combinations of force and distance. In physics, "work" is equivalent to energy, and Work = Fd
1. For each picture, identify the machine (s).
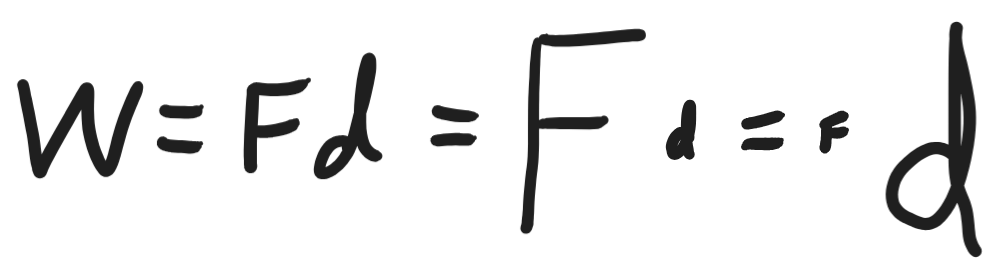 2. For each machine, tell how the machine alters
the distance over which force must be applied by the human using the
machine.
2. For each machine, tell how the machine alters
the distance over which force must be applied by the human using the
machine.
3. How does the machine alter the force that the human must apply?
4. Which "machine" is fundamentally different? Why?
Today:
- Test: Circular Motion and Gravity
Homework:
- None
 Class
36.5: Wednesday,
12/18/24
Class
36.5: Wednesday,
12/18/24Warm Up: How hard would it be to pour a drink during a barrel roll?
Today:
- Hot pink is the color that I used for wrong answers when I graded the corrected rocket project stuff.
- Return retakes
- Do this first --
today is a short class!
- Check/review homework
- Tomorrow's Test:
- 5 Problems:
- Vertical circle (top, bottom, or both)
- Space station simulated gravity problem (essentially a horizontal circle problem)
- g problem
- Law of gravitation problem
- Orbit problem
- No problems requiring the Period (T) formula.
- On the retake, you can retake any individual problem.
- 5 Problems:
Homework:
- Test tomorrow: Circular Motion and Gravity
 Class
36: Tuesday,
12/17/24
Class
36: Tuesday,
12/17/24Warm Up:
1. Which formulas will be provided on the test?
2. Which formulas can be easily derived?
3. For each formula...
a) to what situation does it apply?
b) to what does each letter apply?
Today:
- Test Review
- Optional retake -- 2-D Forces test
Homework:
- Practice Test 2, #1-5. Unit 5 Handout PDF Unit 5 Answer Key
- Videos are in Google Classroom, in the assignment "Class #35.5 Homework Help..."
 Class
35.5: Monday,
12/16/24
Class
35.5: Monday,
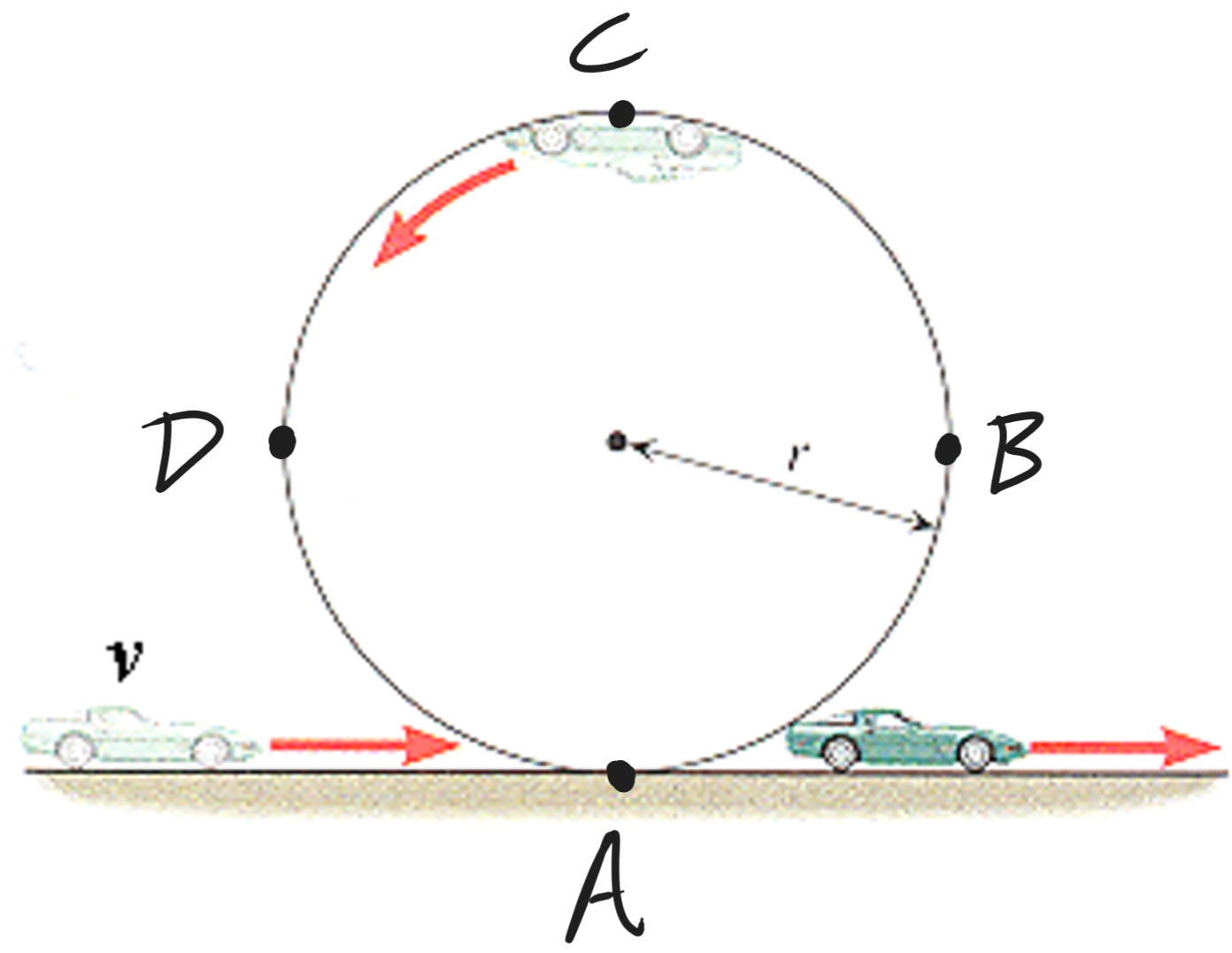
12/16/24Warm Up: The car is driven at a constant speed through the loop-the-loop.
1. Sketch a force diagram for each letter in the diagram. Identify each force.
2. Write an expression for normal force at each letter.
Today:
- Check/review homework
Homework:
- Practice Test 2, #1-5. Unit 5 Handout PDF Unit 5 Answer Key
- Videos are in Google Classroom, in the assignment "Class #35.5 Homework Help..."
Warm Up:
None
Today:
- Mr. Stapleton is out of town.
- Work on the first practice test. Use the solutions and video to check yourself and get help. See "homework, below."
Homework:
- Due on Monday -- Handout p. 5-7 "Practice Test #1" Unit 5 Answer Key Video Explanations Some of the problems have been skipped, since we're leaving out Kepler's laws this year.
 Class
34.5: Thursday,
12/12/24
Class
34.5: Thursday,
12/12/24Warm Up:
1. Why do we have tides?
2.
Why is there a high tide on the opposite side of the Earth from
the Moon?
3. Which object is excerting a greater gravitational force on you right now, the Moon or the Sun?
4. How is this related to black holes?
Today:
- Return tests. Optional retake next Tuesday.
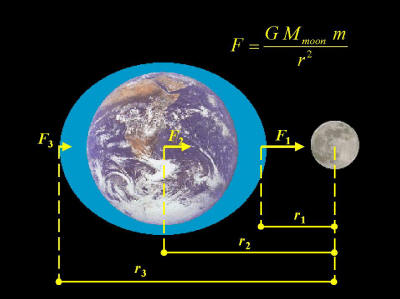
- P. 3-4 of the Unit 5 Handout PDF Unit 5 Answer Key -- using Newton's Law of Gravitation and deriving three useful formulas. Video From Class
- Mr. Stapleton gone tomorrow. Work on the first practice test. Use the solutions and video to check yourself and get help. See "homework, below."
Homework:
- Due on Monday -- Handout p. 5-7 "Practice Test #1" Unit 5 Answer Key Video Explanations Some of the problems have been skipped, since we're leaving out Kepler's laws this year.
Warm Up: None
Today:
- Test -- Forces in 2-D
- Retake next Tuesday.
Homework:
- None
 Class
33.5: Tuesday,
12/10/24
Class
33.5: Tuesday,
12/10/24Warm Up: We don't have to answer all of these.
1. What's the formula for the net force acting on the jogger in the video?
2. Approximately how fast is the jogger in this video moving?
3. If the jogger turned around and jogged the other way, would he feel any different?
4. What must move in order for the person to experience simulated gravity... the space station, the person, neither, or both? What does "move" mean in outer space?
5. There are essentially two ways to simulate 1g of gravity in "outer space." What are they? How are they similar? How are they different? How do they compare to real gravity?
Today:
- Check/review homework
- Work on p. 3-4 of the Unit 5 Handout PDF Unit 5 Answer Key -- Law of Gravitation and combining the law of gravitation with the centripetal force (or acceleration) formula.
Homework:
- Test tomorrow
 Class
33: Monday,
12/9/24
Class
33: Monday,
12/9/24Warm Up:
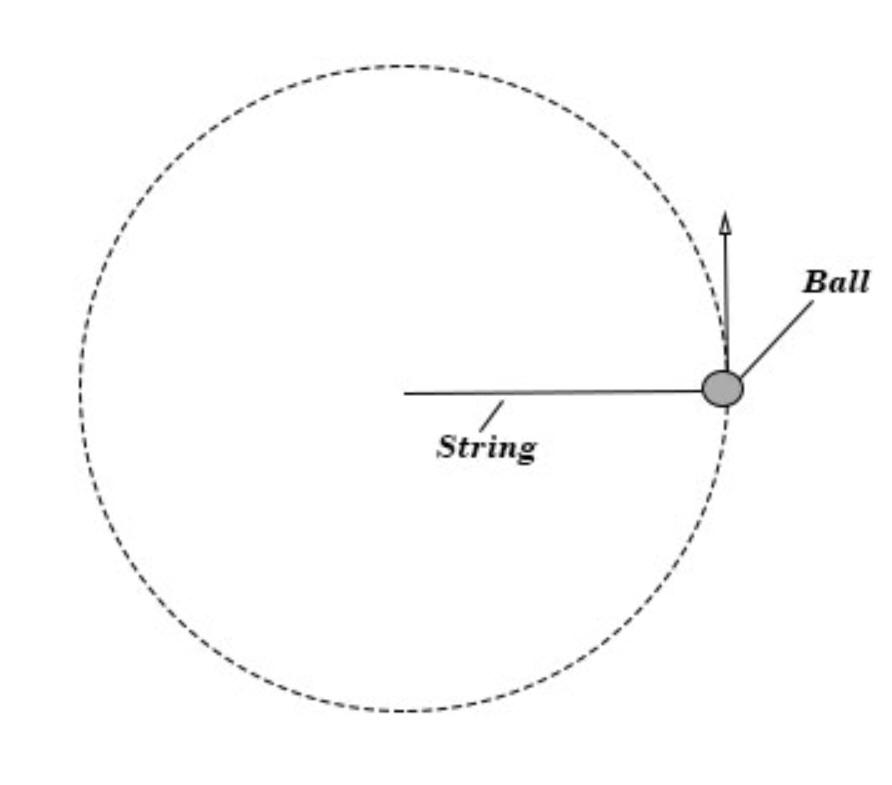
The ball is moving at a constant speed in a circular path.
1. What is the direction of its acceleration?
2. How do we know this?
Today:
- Preview of this week and next
- Check/review homework
- 2D forces test retake next Tuesday.
- Derivation of ac = v2/r (direction and magnitude)
- Start the new Unit -- Circular Motion and Gravity
Unit 5 Handout
PDF
Unit 5 Answer Key --
Video
from Class
- Fix the formulas on the back
- p. 1 and more?
Homework:
- Complete the practice problems on p. 2 of the handout. Unit 5 Answer Key
 Class
32.5: Friday,
12/6/24
Class
32.5: Friday,
12/6/24Warm Up: The drawing on the right shows a top view of a car stuck in mud. A tight chain has been hooked to the car's bumper and also to a large tree. At this point, how could someone (theoretically) move the car forward by applying very little force?
Today:
- Check/review homework
- Return rocket acceleration graphs. Grades should actually be out of 9. I plan to add a point, so the total points for the project is 106 (Graph = 9; Video Analysis = 16; "9 Moments" = 81). The two problems in the video analysis are worth 3 points and 5 points, respectively.
- When you fix your spreadsheets, do not change the colors I have added. Those will tell me which cells I need to re-check.
- Coming Up:
- Test next Wednesday
- Begin Unit 5 (Circular Motion ) on Monday
- Rocket Project corrections are due next Friday.
- Work time
Homework:
- p. 9-12 (22-23 Test Retake) Spreadsheet with answers (and solutions in the form of formulas)
- Videos showing how to do similar problems (these are not the homework problems, but they're the same type of problems.):
 Class
32: Thursday,
12/5/24
Class
32: Thursday,
12/5/24Warm Up: Cheryl wants to use some string and a nail to hang a treasured portrait of great-great-grandfather Ernesto as a young man. The portrait is rather heavy. Rank the three configurations on the right according to their risk of exceeding the breaking strength of the string. (Hint: draw a force diagram with arrows to scale).
Today:
- Check/review homework
- How to do the two remaining types of problems -- p. 6 (#3), then p. 5(#2) Video from class
Homework:
- #2 on p.5 and #4 on p.6
 Class
31.5: Wednesday,
12/4/24
Class
31.5: Wednesday,
12/4/24Warm Up:
A 4 kg mass is suspended by an ordinary string from the ceiling of a fully-enclosed train car (with no vertical movement). The car is on a level surface at sea level, and the angle shown remains constant.
1. How many of these can we deduce from this information?
A) The mass' direction of movement
B) The mass' acceleration
C) The mass' speed
D) The string tension
2. If you wanted to simulate this (i.e. make a mass hang "motionless," at an angle, like this), what would you have to do?
Today:
- Check/review homework
- Solve the warm-up -- find acceleration and tension of a mass hanging from the ceiling: Video from Class
Homework:
- Two number threes: #3 on page 4 and #3 on page 8 of Unit 4 Handout (Forces in 2D) PDF Answers and Solutions
 Class
31: Tuesday,
12/3/24
Class
31: Tuesday,
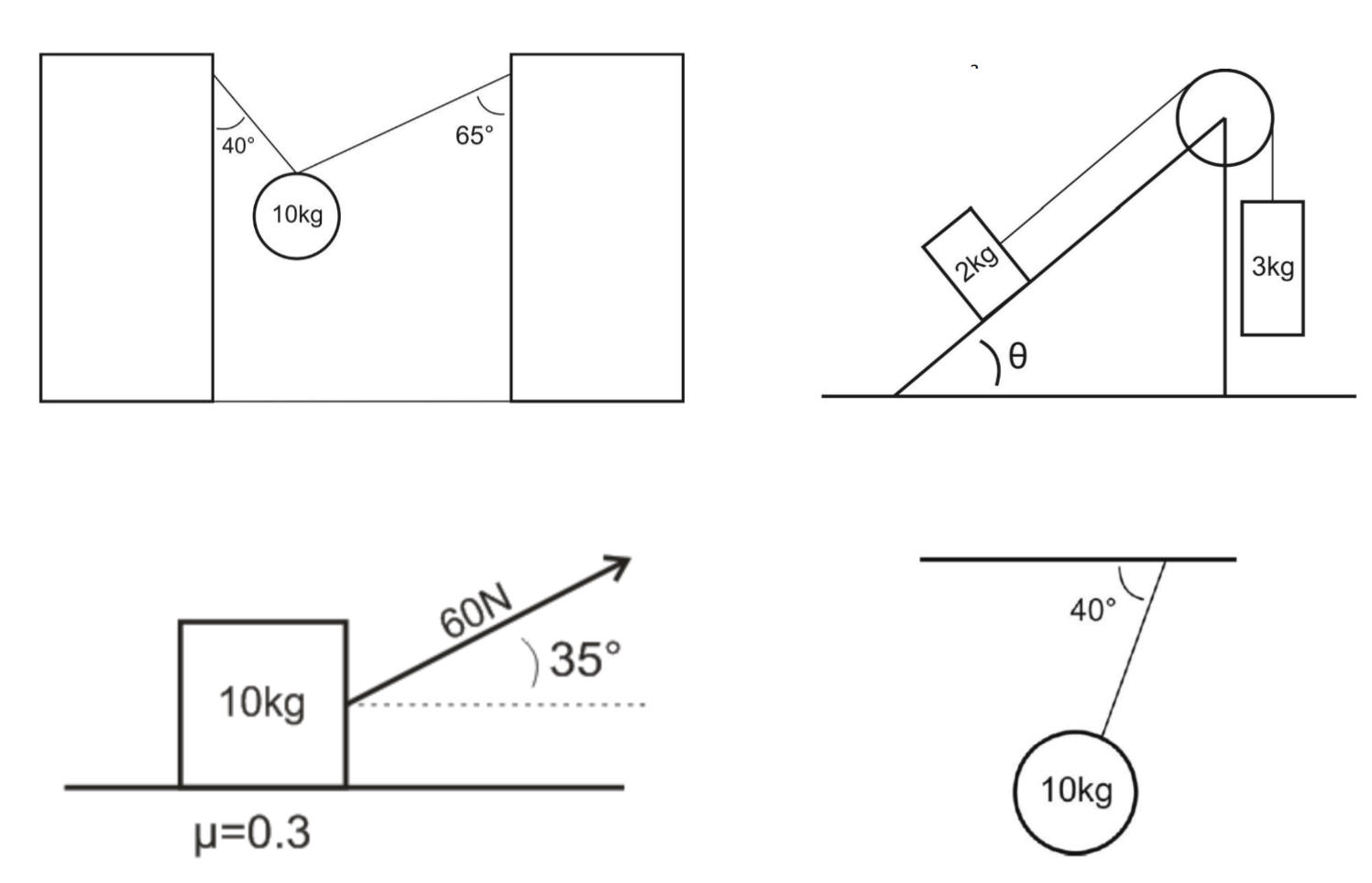
12/3/24Warm Up: In both situations on the right, a block slides along a surface without losing contact with the surface. In past problems, the weight of a block sliding on a surface was always equal to the normal force. For each of these situations, explain why the block's weight and normal force are different.
Today:
- New Stuff:
Unit 4 Handout (Forces in 2D)
PDF
Answers and Solutions
- Work through the problems on pages 1 and 3 together. Video from Today's Class
- Work time
- If you're turning in a hard copy of your graph, turn it in during class today. Or get it to me in C234, during 7/8.
- Don't forget to label your graph points.
Homework:
- Water Rocket Projects are due tonight
- #1 on p. 2 and #2 on p.7 in the Unit 4 Handout (Forces in 2D) PDF Answers and Solutions
 Class
30.5: Monday,
12/2/24
Class
30.5: Monday,
12/2/24Warm Up: In this next short unit, you will be finding all of the forces and accelerations in situations like those shown on the right. What general problem-solving strategy(ies) might be helpful?
Today:
- Preview of what's coming up...
- Forces in 2-D (short unit -- 1 week)
- Circular Motion
- Midterm Exam
- Rocket work time
Homework:
- Finish the Water Rocket Project
Warm Up: If you want help on any particular part of the project, pick a part now, and I'll show you how to do it.
Today:
- Discuss the height at launch and the height at the beginning of coasting.
- Project work time
Homework:
- Projects are due on Tuesday.
Warm Up: How would you measure the force of water rocket thrust, with the rocket pointing upward?
Today:
- If you don't have good data for the water thrust part of the launch, you can use someone else's -- but you should do your own calculations.
- Complete the rest of the water rocket project (handout 2 -- PDF) -- turn it in via Google Classroom (unless you turn in a hard copy of the graph).
- Clifford Heath's Water Rocket Simulator
Homework:
- Optional -- work on the project.
 Class
29: Wednesday,
11/20/24
Class
29: Wednesday,
11/20/24Warm Up:
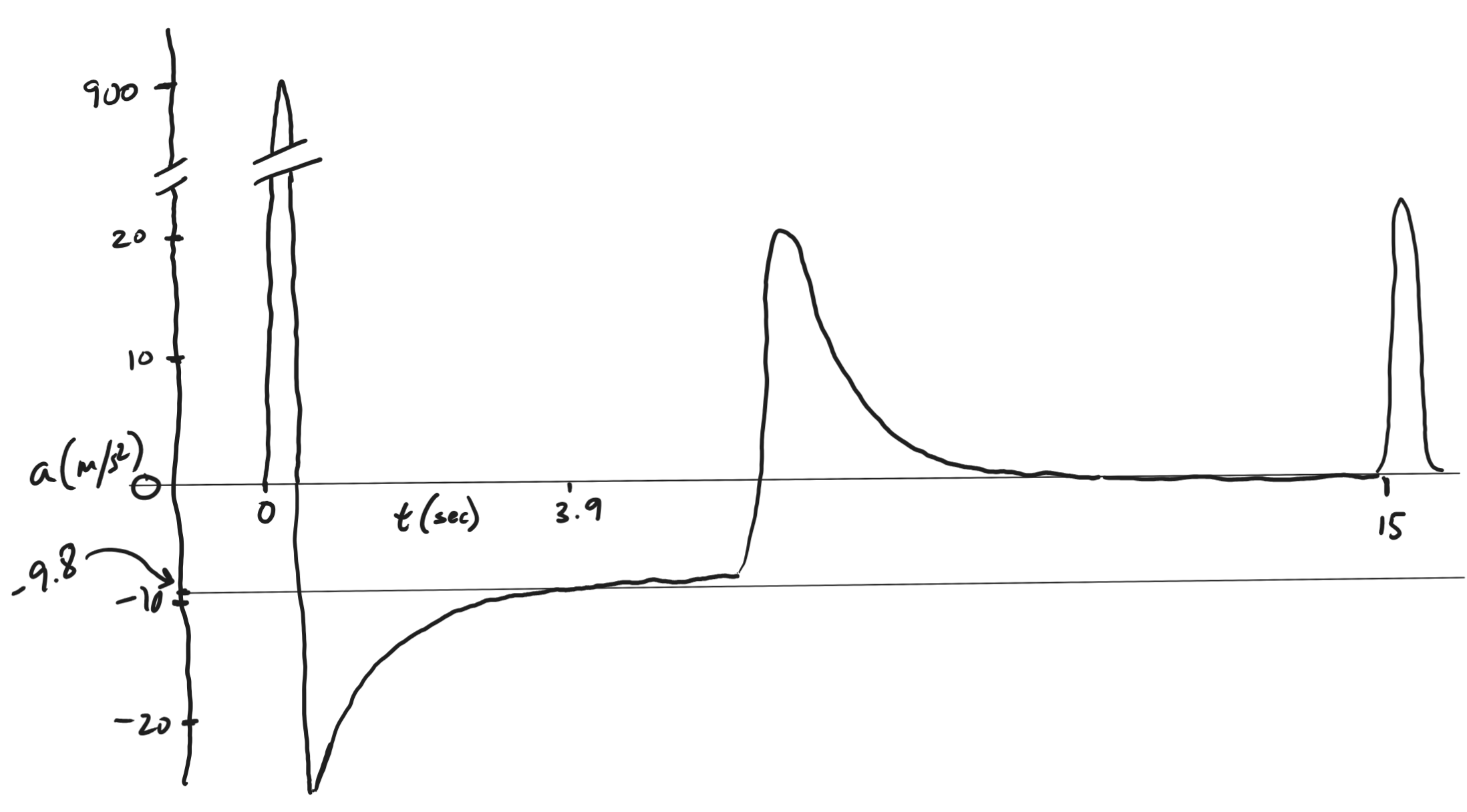
An acceleration graph for a rocket launch with a parachute might look something like this.
1. Locate these moments in time ("snapshots" from the project).
a. sitting on the launch pad
b. Thrust phase
c. Beginning of coasting phase
d. Apogee
e. Moment during descent when net force is highest
f. Just before landing
g. Impact
2. How would this graph look different if there were no parachute?
Today:
- A12 -- share an alternate way to measure time aloft
- Work on the Water Rocket Modeling Project, part 1. Work on
Water Rocket Modeling, Part 1: Video Analysis, Calculations, and Two
Problems (PDF)
- Eventually, you will be entering your answers into this spreadsheet (so that I can easily check them).
- Measure the force of water rocket thrust using a force plate.
Homework:
- Optional -- work on the project.
Warm Up: Open Clifford Heath's Water Rocket Simulator and one of the trajectory spreadsheets that we have been using. Find out what cross-sectional area he uses in his simulation. To do this:
1. Set his simulation to: water volume = 0.6, dry mass = 150g, Cd = 0.3, and pressure = 100p.
2. Run his simulation and find his rocket's initial coasting speed by adding the burnout velocity to the speed increase due to air pulse.
3. Set your spreadsheet air density to 1.23kg/m3 (approximately average)
4. Use his burnout height as your initial y position, and match your other spreadsheet initial parameters to his.
5. Adjust your cross-sectional area until your time aloft matches his.
Today:
- Decide on your rocket's cross-sectional area. Then
disassemble your rocket.
- Duct tape in the trash
- Rebar (with hot glue removed) in the peanut butter jar
- Intact bottles in a bag
- clean plastic pieces in one of the box lids
- Put extra caps on bottles
- Begin the Water Rocket Modeling Project. Work on
Water Rocket Modeling, Part 1: Video Analysis, Calculations, and Two
Problems (PDF)
- Eventually, you will be entering your answers into this spreadsheet (so that I can easily check them).
Homework:
- Optional -- work on the project.
Warm Up: None
Today:
- Test retake
- Work time (if you haven't finished the spreadsheet homework)
Homework:
- Check your Spreadsheet Quiz answers. If you missed any, and you don't know why, watch this video. If you still have questions, ask them on Tuesday.
Warm Up: Prepare to launch
- Measure your rocket's dry mass and record it.
- Carefully add 600ml of water to your rocket.
- Prepare to record
launch videos
- Make sure that your camera is recording at 240fps.
- Hold your camera in landscape orientation.
- Adjust your field of view. The bottom should be even with the launcher base, and the top should be 3m above the base.
- Keep the camera motionless until the rocket leaves the launch field of view, then follow the rocket. You may need to zoom out to find it. It doesn't need to be large -- just visible.
- Follow the rocket until its moment of impact.
Today:
- Launch.
- Back in the classroom,
- Estimate your rocket's cross-sectional area.
- Make a copy of your video that just shows the initial launch, completely in slow motion. Email this to yourself and your partner(s).
- Save the video
Homework:
- Test retake on Monday
- Check your Spreadsheet Quiz answers. If you missed any, and you don't know why, watch this video. If you still have questions, ask them on Tuesday.
 Class
27: Thursday,
11/14/24
Class
27: Thursday,
11/14/24Warm Up: What's the best amount of water to put in a water rocket? [Find out, according to Clifford Heath.] How does the amount of water affect force and overall acceleration?
1. What happens if you don't add any water?
2. What happens if you completely fill the rocket with water?
Today:
- Finish rockets and launch
- Measure your rocket's dry mass.
Homework: Spreadsheet problems in Google Classroom
Warm Up: How can you make nice, straight, recyclable fins out of a 2-liter bottle?
Today:
- Test retake on Monday!
- Check/review homework
- Start building rockets. Here's a basic design...

- Make sure that your pressure chamber fits on the launcher (have Mr. Stapleton check).
- Make sure that nothing intereres with the launcher jaws.
Homework: If you have a smartphone that takes slow motion video, get prepared to take videos next class. Here's how to do it on an iphone (if you have an Android, maybe someone else has suggestions)...
- Shut down and restart your phone (otherwise your fps settings might be out of whack)
- Open settings
- Open camera
- In "record slo-mo" set to 720p at 240fps (NOT high efficiency)
- In "Format," choose "most compatible." [so you can open the videos in vernier video analysis]
 Class
26: Tuesday,
11/12/24
Class
26: Tuesday,
11/12/24Warm Up:
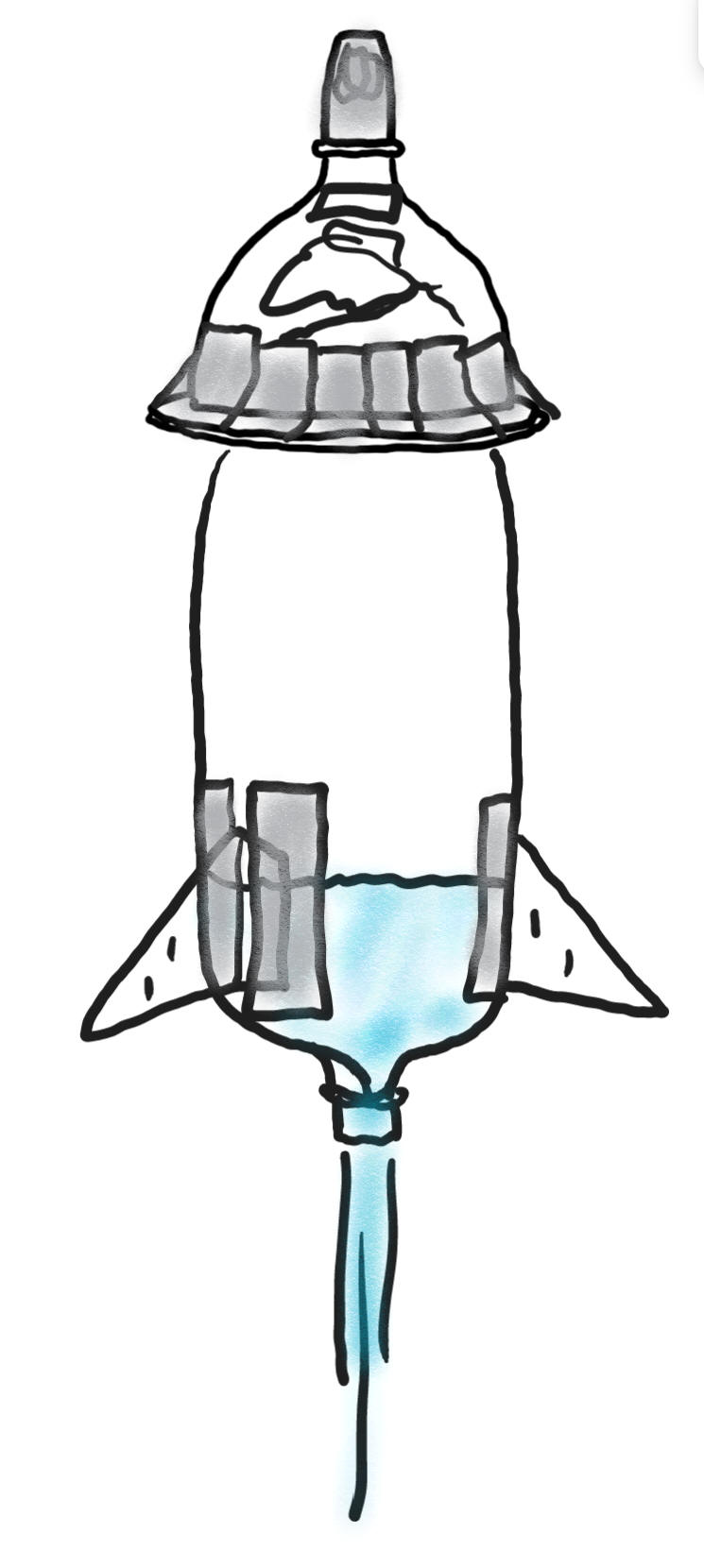
The diagram on the right shows a 2-liter bottle water rocket. Mass has been added to the tip of the rocket's nose cone, and fins have been added to the back (bottom). The nose cone sits loosely on a platform that is hidden beneath the nose cone's flange. The nose cone and pressure chamber are not fused together, but they are connected by a string, which also connects to the parachute. Video of one rocket another video
1. What makes the rocket move upward?
2. Why do fins need to be added to the back of the rocket? How does this work?
3. Why does mass needed to be added to the front of the rocket? How does this work?
4. Aside from stability, what other reason is there for adding mass to the rocket?
5. What's the purpose for the flange at the bottom of the nose cone?
Today:
- Debug the spreadsheets
- Use your spreadsheet to find the drag coefficient of a ping pong
ball. Use the data below, which correspond to the
table
tennis ball drop video:
- Y displacement = -4.9m
- Air density = 1.253 kg/m3
- Mass = 0.00189kg
- Drop time = 1.167s
- Cd =
- A1 Class Data: Vertical, upward table tennis ball launch:
- Ball Mass = 0.00189kg
- Ball Diameter = 4cm
- Air Density = 1.277126 kg/m3
- Y displacement = -2.33m
- Time aloft = 4.08s
- Initial Speed, based on 0.005s time increments = 205m/s
- A2 Class Data: Vertical, upward table tennis ball launch:
- Air temperature (F) =
- Air pressure (inHg) =
- Relative Humidity =
- Air Density (kg/m3) =
- Y displacement =
- Time aloft =
- Make a modified version of the spreadsheet that is better for completing the homework assignment
- Tomorrow -- Build Rockets:
- Goal: design and build a rocket with the lowest drag
coefficient
- Uses no more than 1m of duct tape
- Has a piece of rebar at the tip
- Is designed to be taken apart, so that parts can be reused next year.
- We're not doing parachutes this year, but some of these videos are probably still useful. Especially the one(s) about fins Construction playlist
- Here's a simulatorClifford Heath's simulation.
- Goal: design and build a rocket with the lowest drag
coefficient
Homework: Using your spreadsheet and the data collected in class (details above), find:
- Using the same velocity from #1, find the launch angle that gives a maximum range.
- If the same ball were launched horizontally at the speed of sound (use 343m/s), how far, horizontally, would it have to travel before slowing down to 50m/s?
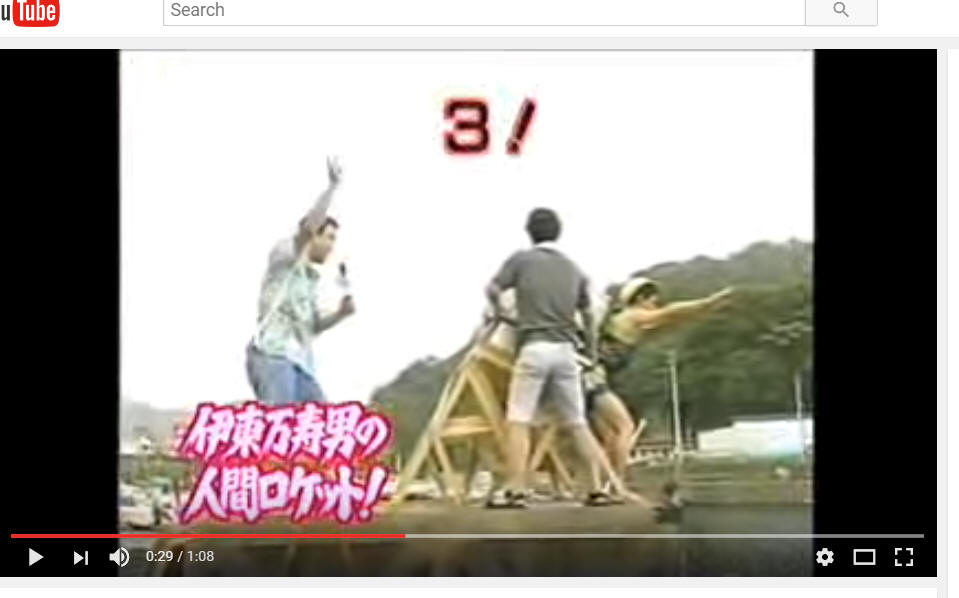 Class
25.5: Monday,
11/11/24
Class
25.5: Monday,
11/11/24Warm Up:
1. What force launches this game show contestant?
2. Is this for real? Could we launch a student this high? How could we find out?
Today:
- Return tests
- Debug the spreadsheets
Homework: None
Warm Up: None
Today: Test
Homework: None
 Class
24.5: Thursday,
11/7/24
Class
24.5: Thursday,
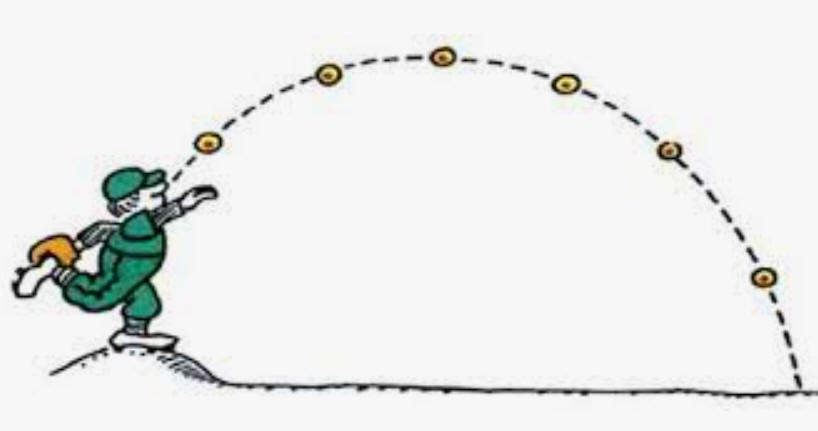
11/7/24Warm Up: In the absence of air resistance, the flight of a projectile looks like the picture on the right. What does it look like with air resistance?
Today:
- Test review?
- Investigations with the spreadsheet and ping pong balls (mostly)
- Cd of a ping pong ball
- Speed of air exiting a shop vac
- Speed of a ping pong ball launch
- Optimal ping pong ball launch angle -- for greatest range
Homework: Unit 3 Answer Key
- Prepare for tomorrow's test
 Class
24: Wednesday,
11/6/24
Class
24: Wednesday,
11/6/24Warm Up: If you need to stop a car quickly, why should you avoid locking the tires or skidding?
Today:
-
Stuff related to Friday's test
-
If you look at last year's classes 29.5 and 30, I listed some test topics that also apply this year.
-
Questions?
-
Create a spreadsheet to analyze a projectile (e.g. a coasting rocket) that is experiencing drag. StapletonExample
-
Explain the seemingly strange aspects
-
Homework:
- Turn-in a copy of your spreadsheet to Google Classroom


 Class
23.5: Tuesday,
11/5/24
Class
23.5: Tuesday,
11/5/24Warm Up: I have a length of treated 4"x4" lumber, some large nails, a hammer, and a large rock. How will it feel if I put the rock on my head and then have someone pound nails into the wood on top of the rock?
Today:
- Check/review homework
- Unit 3 Handout (PDF)
- Go over the test format.
Homework: Unit 3 Answer Key
- None. Prepare for the test. Write down questions that you would like to ask.
 Class
23: Monday,
11/4/24
Class
23: Monday,
11/4/24Warm Up: The harpoonist in the diagram is accelerating in both the X and Y dimensions. Draw a diagram showing all of the individual and net forces acting on the harpoonist. Then find the X acceleration of the Harpoonist.
Today:
- Check/review homework
- Practice test work time. Treat it like a real test.
Homework: Unit 3 Answer Key
- Practice Test -- p. 21-24
- Test on Friday (11/8)
 Class 22.5: Thursday,
10/31/24
Class 22.5: Thursday,
10/31/24Warm Up: Ryan Crouser (approximately 145kg -- not the guy in the picture) set a world record by throwing a 7.26 kg shotput 23.51m.
1. Estimate the speed of the shotput when it left his hand. This can be quick.
2. Draw a system schema for the point in time where he is pushing the shotput with the greatest force.
3. Draw a force diagram showing all of the forces acting on Ryan at that time. Estimate the forces.
Today:
- Check/review homework
- Unit 3 Handout (PDF)
- Work time
Homework: Unit 3 Answer Key
- p. 19-20, 1-6 only (not #7 on p.20)
 Class
22: Wednesday,
10/30/24
Class
22: Wednesday,
10/30/24Warm Up:
1. How fast does chalk fall? Is it faster than a cat?... (My spreadsheet answer) Why?
2. Sometimes people celebrate special occasions by firing guns into the air. Is this safe?
3. Why don't clouds fall out of the sky?
Calculated terminal velocities of various spheres.
Today:
- Check/review homework
-
Practice drawing force diagrams
(PDF) Solutions:

- Unit 3 Handout (PDF)
- Work time
Homework: Unit 3 Answer Key
- p. 17-18 -- on page 18, change the astronaut weight in #1 to 2,000N from 600lbs
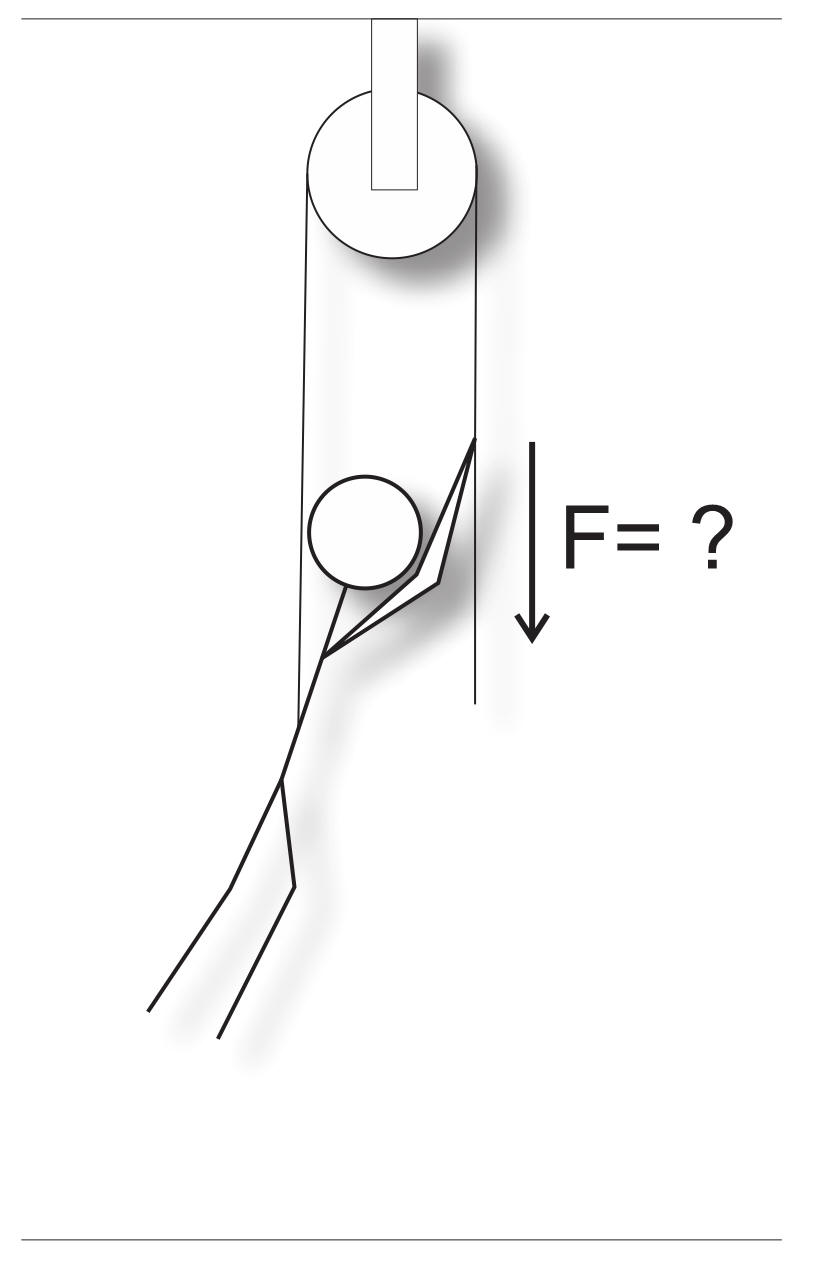 Class
21.5: Tuesday,
10/29/24
Class
21.5: Tuesday,
10/29/24Warm Up: One end of a rope is attached to the Gladys' belt. Gladys is pulling directly downward on the other end. Assuming that the pulley and rope are massless and fictionless, how much downward force must Gladys apply in order to ascend? Gladys weighs 500N.
Today:
- Check/review homework
- If there's time, sketch force diagrams (individual forces and
net force) for each of the following:
- A person standing in an elevator that is starting to ascend
- A person playing tug-of-war, beginning to be pulled to the right.
- A trampolinist flying upward through the air after jumping
- Someone standing in a a cruise ship that is traveling rightward but is slowing down due to an iceberg collision
- Someone throwing a shotput to the left
- A rower in a boat's galley, moving righward at a constant speed while rowing the boat rightward
- Unit 3 Handout (PDF)
- Work time
Homework: Unit 3 Answer Key
- p.14 #1-4
- p. 16, #8
 Class
21: Monday,
10/28/24
Class
21: Monday,
10/28/24Warm Up:
According to this article, emergency clinic records of 132 cats that jumped from windows of buildings showed a 90% survival rate. The average drop was 5.5 floors.
1. What's going on?
2. When does a falling cat experience zero net force?
3. When is a falling cat a "free-falling" cat?
4. When does a falling cat experience maximum net force?
5. What characteristics of an object contribute to its drag (a force resisting movement through fluids)?
Today:
- Return quizzes. Retake at the beginning of any class.
- Check/review homework
- B2 -- finish the multibody practice problem on page 10 Unit 3 Handout (PDF)
- Drag and Terminal Velocity Notes (p.12-13) Unit 3 Answer Key 2021 Notes Video -- Start at 15:48.
Homework: Unit 3 Answer Key
- P. 11, problems 4-6.
- p. 15, #5
 Class
21.5: Friday,
10/25/24
Class
21.5: Friday,
10/25/24Warm Up: Find the acceleration of the system on the right and the tensions in the two strings. Assume that the entire system is frictionless and that the pulleys and strings are massless.
Today:
- Check/review homework -- use this spreadsheet to check your answers Orders of magnitude (length) link.
- Quiz over kinematics formulas -- will go on Q2
- B2 example multibody system problem
Homework:
- Problems 1-3, on packet pages 10-11. Unit 3 Answer Key Video of Solutions
- If you haven't done it already, use this spreadsheet to check your Newton Sled problems. Identify anything you want to ask about next class.
 Class
21: Thursday,
10/24/24
Class
21: Thursday,
10/24/24Warm Up: The 2nd diagram on the right is a System Schema representing the situation in the top diagram, where the "objects of focus" are the blocks. For simplicity, the creator of the diagram has assumed that the blocks are frictionless but the person is still pushing them somehow.
1. What is a system, in Physics?
2. What does a system schema show? In a system schema, what is the difference between the "objects of focus" and the other objects?
3. How can a system schema clarify the application of Newton's 2nd and 3rd Laws to solving problems in situations like this?
4. Let's create one for this
situation, with the objects of focus being the book and apple.

5. ... and another one for this situation: a chair is pushed across the floor by a student, with realistic friction. Assume that the student and chair are both objects of interest.
6. Use one of the previous system scheme (4 or 5) to create a "free body" diagram showing the forces acting on one of the objects of interest.
Today:
- Check/review homework -- Newton Sleds #6.
- Notes p. 8-10: tension, systems, and multibody problems Unit 3 Handout (PDF) Video from pages 8-9 -- Systems
- Video: suggestions for completing the sled problem
- Work time
Homework:
- Complete the Newton Sled Activity Newton Sled Activity PDF Problem organizer PDF
- Memorize the kinematics formulas (and the range formula).
Quiz tomorrow. The quiz will be "write the 6
basic kinematics formulas, plus the range formula." The
answers will be
 .
You can have unlimited retakes of this quiz, but you may have to
come to FLEX for some of them.
.
You can have unlimited retakes of this quiz, but you may have to
come to FLEX for some of them.
 Class
20.5: Wednesday,
10/23/24
Class
20.5: Wednesday,
10/23/24Warm Up: The rower in the photo has a mass of 50kg and a leftward acceleration of 1m/s2. She is pulling against the oars with a total force of 100N. Sketch a diagram showing all of the forces acting on the rower. Find all of the forces' magnitudes.
Today:
- Check review homework.
- Check and make sure that we have problem-solving step zero in your notes.
- Finish #6 of the Newton Sled Activity
Homework:
- #6 A and B of the Newton Sled Activity
- Memorize the kinematics formulas (and the range formula).
Quiz on Friday. The quiz will be "write the 6
basic kinematics formulas, plus the range formula." The
answers will be
 .
You can have unlimited retakes of this quiz, but you may have to
come to FLEX for some of them.
.
You can have unlimited retakes of this quiz, but you may have to
come to FLEX for some of them.
 Class
20: Tuesday,
10/22/24
Class
20: Tuesday,
10/22/24Warm Up: On level ground, Tim begins sliding with a velocity of 6m/s. If Tim's slide lasts for 2 seconds...
1. What is the coefficient of kinetic friction between Tim and the slide?
2. What is the broader implication, if we compare the acceleration due to friction and the acceleration of gravity, on level surfaces?
Today:
- Finish reviewing homework -- and check again
- Newton Sled Activity PDF -- Discuss #1-5 in class. Complete #6 for homework.
Homework:
- Complete questions 1-5 and part A only of Problem #6 from the Newton Sled Activity PDF
- Memorize the kinematics formulas (and the range formula).
Quiz on Friday. The quiz will be "write the 6
basic kinematics formulas, plus the range formula." The
answers will be
 .
You can have unlimited retakes of this quiz, but you may have to
come to FLEX for some of them.
.
You can have unlimited retakes of this quiz, but you may have to
come to FLEX for some of them.
 Class
19.5: Monday,
10/21/24
Class
19.5: Monday,
10/21/24Warm Up: The McMurtry Speirling can accelerate from 0-60mph in 1.4 seconds. Its mass is less than 1,000kg.
1. Assuming that the car's acceleration is constant, what is the coefficient of friction between the car tires and the road?
2. Is this the kinetic friction or static friction? How do you know?
3. Actually, this can can accelerate that fast with a coefficient of static friction closer to 0.7. How is that possible?
Today:
- Return retakes
- Check/review homework
Homework:
- None -- If you didn't finish page 16 (#1-7), finish it tonight. Unit 3 Answer Key
Warm Up: None
Today:
- Optional Test Retake: Take as many of the pages as you want -- even if you didn't take them all the first time.
Homework: DUE ON MONDAY
- P. 6 #12-14
- P. 16, #1-7
- Unit 3 Answer Key
 Class
18.5: Thursday,
10/17/24
Class
18.5: Thursday,
10/17/24Warm Up:
One way to find the center of mass (a.k.a. balance point) of a stick is to support it with two hands and then slowly move those two hands together until they meet under the stick's center of mass.1) Try it
2) Explain what's happening, in terms of static friction and kinetic friction?
Today:
- Check/Review homework VIDEO explaining homework solutions
- Unit 3 Handout (PDF) Unit 3 Answer Key
- Notes: Tension (p. 8).
- Questions about tomorrow's retake?
- Work time.
Homework: DUE ON MONDAY
- P. 6 #12-14
- P. 16, #1-7
- Unit 3 Answer Key
 Class
18: Wednesday,
10/16/24
Class
18: Wednesday,
10/16/24Warm Up: Newton's 3rd Law tells us that forces always come in pairs, and that each force in a pair is equal to and opposite the other. If that's true, how do you win at the game of tug of war?
Today:
- Check/Review homework
- Unit 3 Handout (PDF) Unit 3 Answer Key
- Notes: 3rd Law and Friction (p. 6-8) Video of notes
- Work time.
Homework:
- P. 3, conceptual question #3.
- P. 5-6, Problems #8-11. Unit 3 Handout (PDF) Unit 3 Answer Key VIDEO explaining homework solutions
- Test retake on Friday
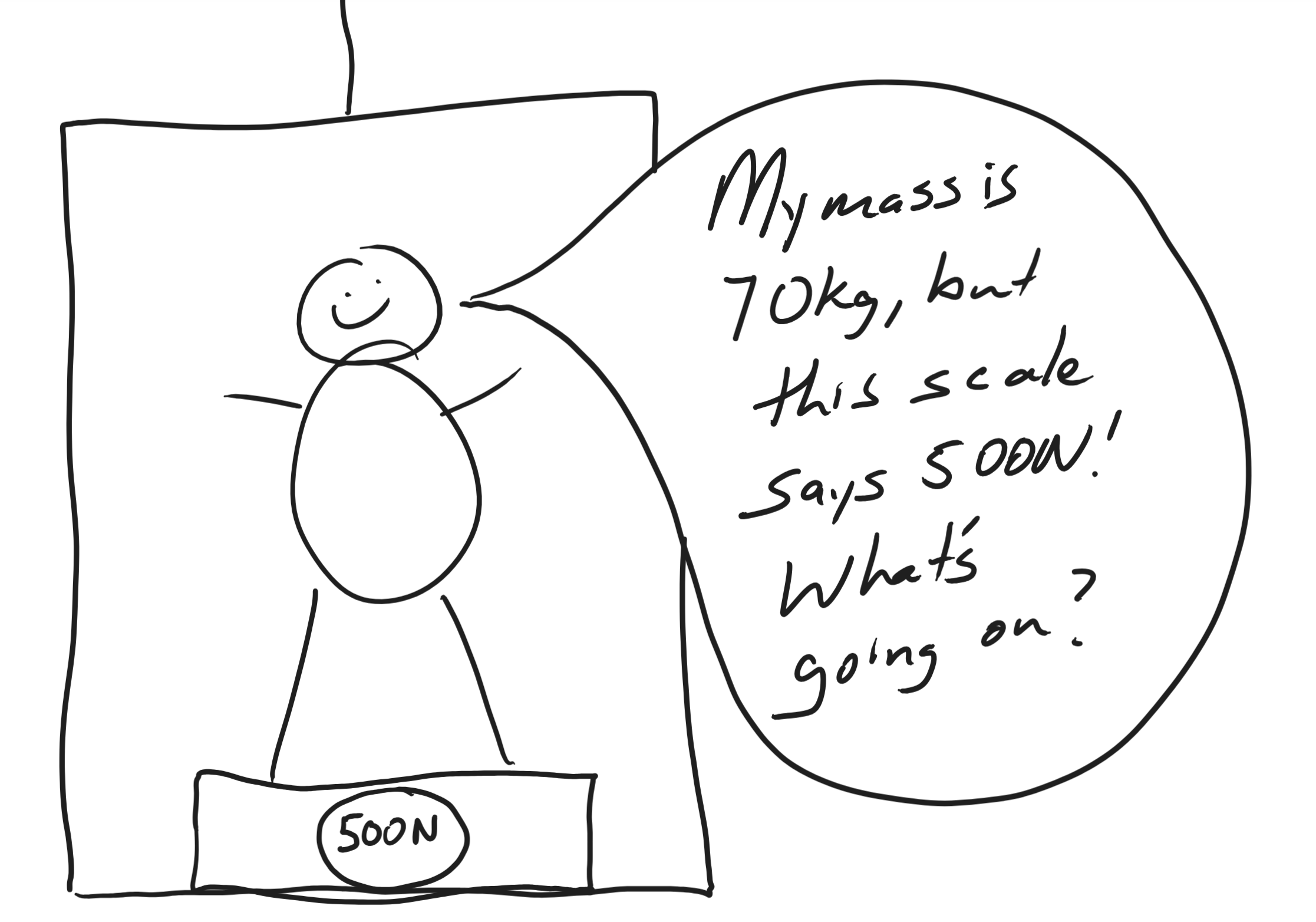 Class
17.5: Tuesday,
10/15/24
Class
17.5: Tuesday,
10/15/24Warm Up: video from class
A common occurrence in physics problems is someone standing on a bathroom scale inside an elevator.
1. Sketch vectors representing all of the forces (pushes or pulls) that are acting on the person in the elevator.
2. Write Newton's 2nd law (applied to the person) and plug in any values that you can.
3. Write an equation for net force as the vector sum of all of the forces acting on the person.
4. Set those two expressions of net force (net force as m*a and net force as the vector sum of forces) equal to one another and solve. Figure out what's "going on."
Today:
- Check/Review homework
- Unit 3 Handout (PDF) Unit 3 Answer Key
- Practice problems -- a tension problem, a normal force problem, and a kinematics problem A1 Class practice problem video A2 Class practice problem video
- Work time.
Homework:
- P. 4-5, Problems #4-7. Unit 3 Handout (PDF) Unit 3 Answer Key
- Test retake on Friday
 Class
17: Monday,
10/14/24
Class
17: Monday,
10/14/24Warm Up: Monkey and Hunter problem:
A green hunter and a blue hunter point their Nerf guns directly at a orange monkey and then fire simultaneously. Just as the two hunters fire their guns, the monkey slips and freefalls from the treetop to the ground. Assuming that this takes place in a vacuum, whose (if anyone's) projectile hits the monkey?
Today:
- Review homework
- Go over the Tunmay Bike Jump bonus problem.
- Notice the test retake practice problems I added to Google Classroom.
- Get the Unit 3 Handout (PDF) Unit 3 Answer Key
- Notes on 1st and 2nd Laws. Video from today's class.
Homework:
- Conceptual questions #1-2 and Problems #1-3 on pages 3-4 of the Unit 3 Handout (PDF) Unit 3 Answer Key
- Test retake on Friday
Warm Up: TBD
Today:
- PSAT day. Most students will be gone.
Homework:
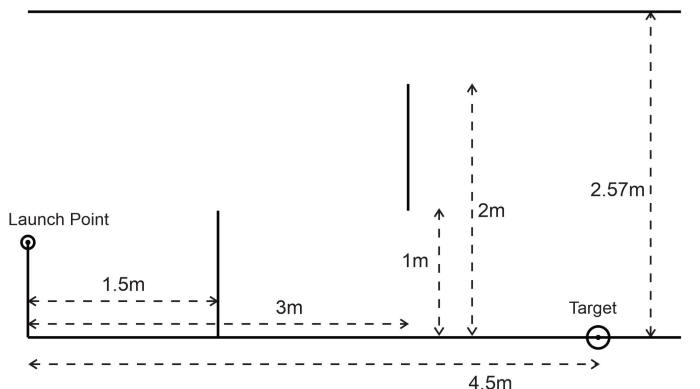 Class
16: Tuesday,
10/8/24
Class
16: Tuesday,
10/8/24Warm Up: If you wanted to launch a projectile from the launch point on the right, so that you would hit the target -- without hitting the ceiling or either of the two obstacles -- what launch angle and speed would you use?
This is a good application for a spreadsheet like this one.
Today:
- Work on projectile motion spreadsheets
- Google Classroom Spreadsheet -- Projectile Motion Problems
- Projectile Motion With Drag
Homework:
- Complete the "Projectile Motion Problems Spreadsheet" in Google Classroom.
- Prepare for the test retake (next Friday -- 10/18)
 Class
15.5: Monday,
10/7/24
Class
15.5: Monday,
10/7/24Warm Up: We have some new Vernier Force Plates. What experiment(s) could we try with one?
Today:
- How to make a spreadsheet
Homework:
- None
Warm Up: None
Today:
- 70 minutes for the test -- pep rally today
Homework:
- None
 Class
14.5: Thursday,
10/3/24
Class
14.5: Thursday,
10/3/24Warm Up: Is it literally possible to "pull yourself up by your own bootstraps?" You may assume superhuman strength and/or speed. Explain.
Today:
- A1/2 -- return retakes
- Check/review the homework.
- Test review -- update: Due to the short class, I removed all but 6 of the short answer/multiple choice section.
- If we run out of test review ideas... create a projectile motion spreadsheet. We will modify it later to include drag.
Homework:
- Prepare for the test.
- Know all formulas and variables (memorize if you can)

- Know 1m/s = 2.24mph
- Review problem-solving strategies for the types of problems that will be on the test (see class 13.5, below).
- Be aware of the "givens" that aren't really given in projectile problems.
- Be able to add and resolve vectors in a variety of situations (projectile motion, river problems...)
- Know all units
- Know all formulas and variables (memorize if you can)
 Class
14: Wednesday,
10/2/24
Class
14: Wednesday,
10/2/24Warm Up: It is possible to remove a sheet paper from under a dry erase pen without touching or tipping the pen. How can one do this without tipping the pen? Why does the pen usually fall? What kind of pen would work better?
Today:
- Check/review the homework that I forgot to check yesterday.
- Test review?
- If we run out of test review ideas... create a projectile motion spreadsheet. We will modify it later to include drag.
Homework:
- Pages 19-20 of the Unit 2 Packet (PDF) Unit 2 Answer Key
- Explanatory videos -- use these if you get stuck
- P.19
- P. 20
 Class
13.5: Tuesday,
10/1/24
Class
13.5: Tuesday,
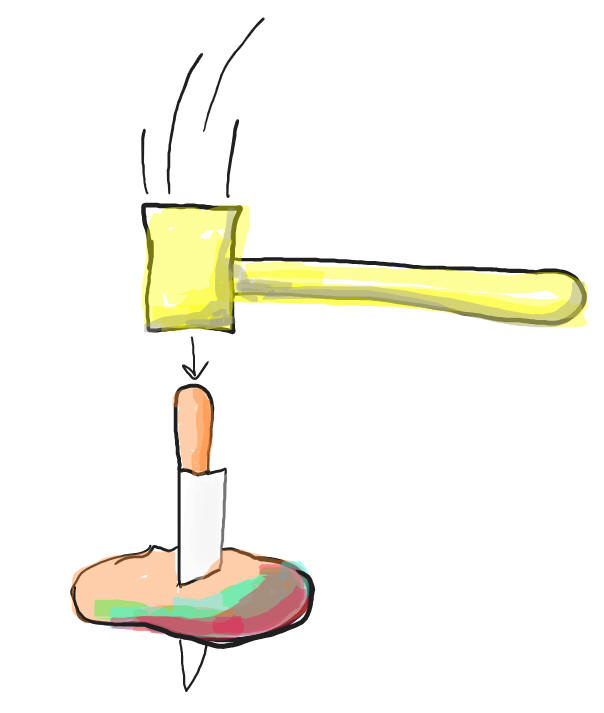
10/1/24Warm Up: What will happen if I poke a knife through a potato, hold both objects in the air with the knife pointing downward, and then hammer the butt of the knife into the potato? Why? What if it's an apple, because I didn't have potatoes?
Today:
- Check/review the homework that I forgot to check yesterday.
- Review the spreadsheet solutions
- Test format:
- 10-15 6 short answer/multiple choice
- 2 River problems with multiple parts (one orthogonal, one non-orthogonal)
- 3 Projectile motion problems, each with multiple parts
- Symmetric, Asymmetric, 1/2 Symmetric.
- Next Unit -- Forces (Newton's Laws)
- What sort of review help do you need?
- Unit 3 Handout (PDF)
Homework:
- Be ready for the test on Friday. If you have questions about the test, we can discuss them. Write down any questions that you have and share them tomorrow.
 Class
13: Monday,
9/30/23
Class
13: Monday,
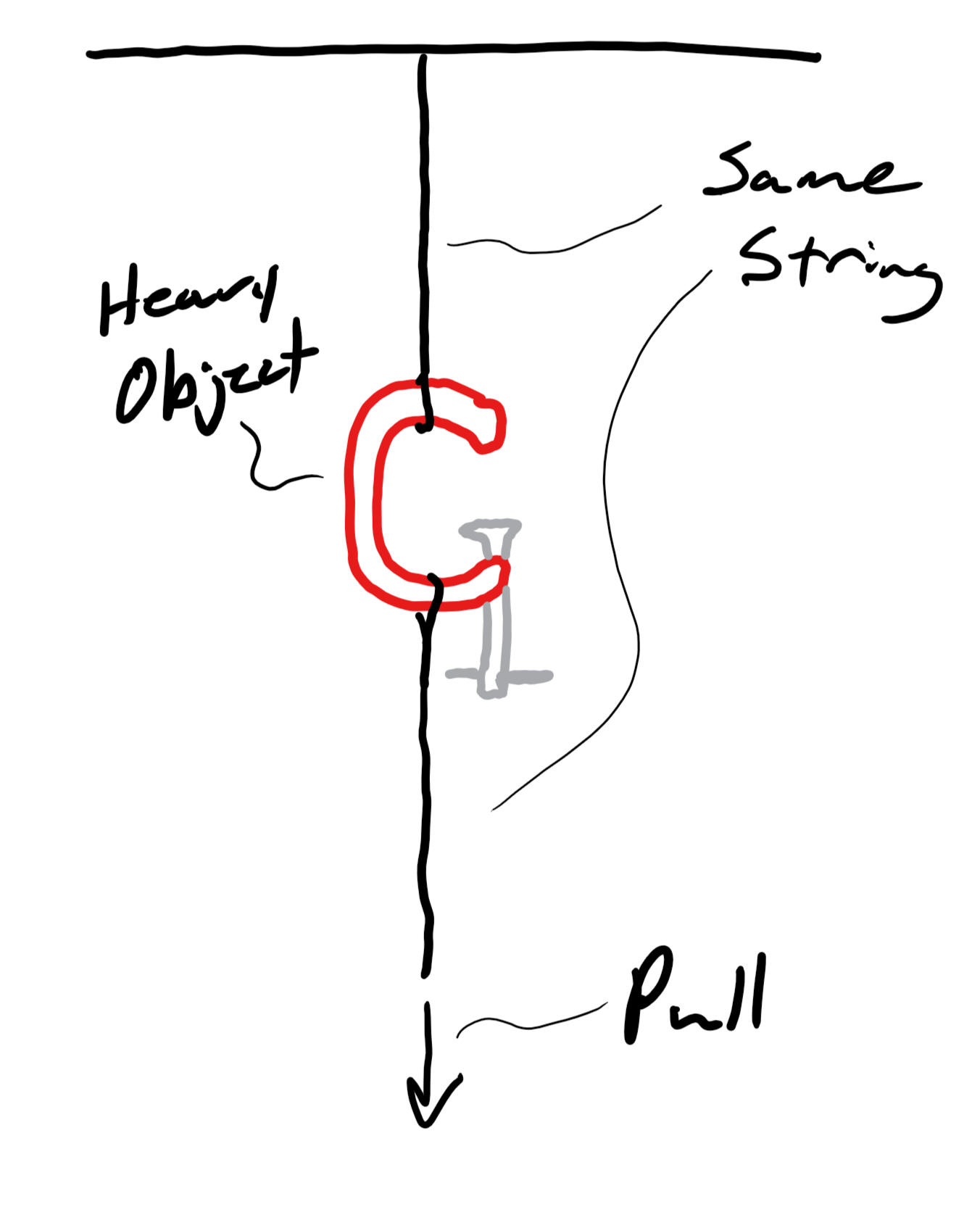
9/30/23Warm Up: There is a heavy object suspended from the ceiling by a string. Another segment of the same string is hanging downward from the object. I am going to pull on the bottom string until one of the two strings breaks. Which string is going to break first? Why?
Today:
- Check/review the homework.
- Finish the launcher challenge from last Thursday. Hit a target on the wall, 1.2m from the floor, with a projectile launched at 10m/s and an angle of 35 degrees -- the projectile must be descending when it hits the wall. While you're at it, find out everything else about this launch. Complete this updated spreadsheet. Get the updated one.
- Tomorrow -- start something new and/or test review. We can review more on Thursday
Homework:
- Finish your spreadsheet and turn in to Google Classroom
- Test Friday
 Class
12.5: Friday,
9/27/24
Class
12.5: Friday,
9/27/24Warm Up: These are all of the variables that can be involved in projectile problems. In the y dimension, all of our kinematics equations can be used.
1. What equations can be used to solve for things the x and the "x&y" dimensions? [Note: I've been saying there's only one formula for the x dimension, but that's not entirely true.]
2. Projectile problems can be classified as symmetric, asymmetric, or "half of a symmetric" problems. Give an example of each.
3. Let's solve one. Problem from A1 Class Problem from A2 Class
Today:
- Check/review the homework.
- My plan is to have the test next Friday, but that's the pep rally day. We could have it on Wednesday, instead. What are your preferences?
Homework:
- Pages 15-16 of the Unit 2 Packet (PDF) Unit 2 Answer Key
- Explanatory videos -- use these if you get stuck
 Class
12: Thursday,
9/26/24
Class
12: Thursday,
9/26/24Warm Up:
1. How does NASA simulate weightlessness?
2. Is this really weightlessness?
Today:
- Discuss recycling and composting
- Check/review the homework.
- Finish the projectile launcher challenge.
- New challenge. Hit a target on the wall, 1.2m from the floor, with a projectile launched at 10m/s and an angle of 35 degrees. You must fire two shots -- one Complete this spreadsheet.
Homework:
- Mr. Pennington's test p.14, Problems #4-6 #4 video #5 video #6 video
- Unit 2 Packet (PDF) Unit 2 Answer Key
 Class 11.5:
Wednesday,
9/25/24
Class 11.5:
Wednesday,
9/25/24Warm Up:
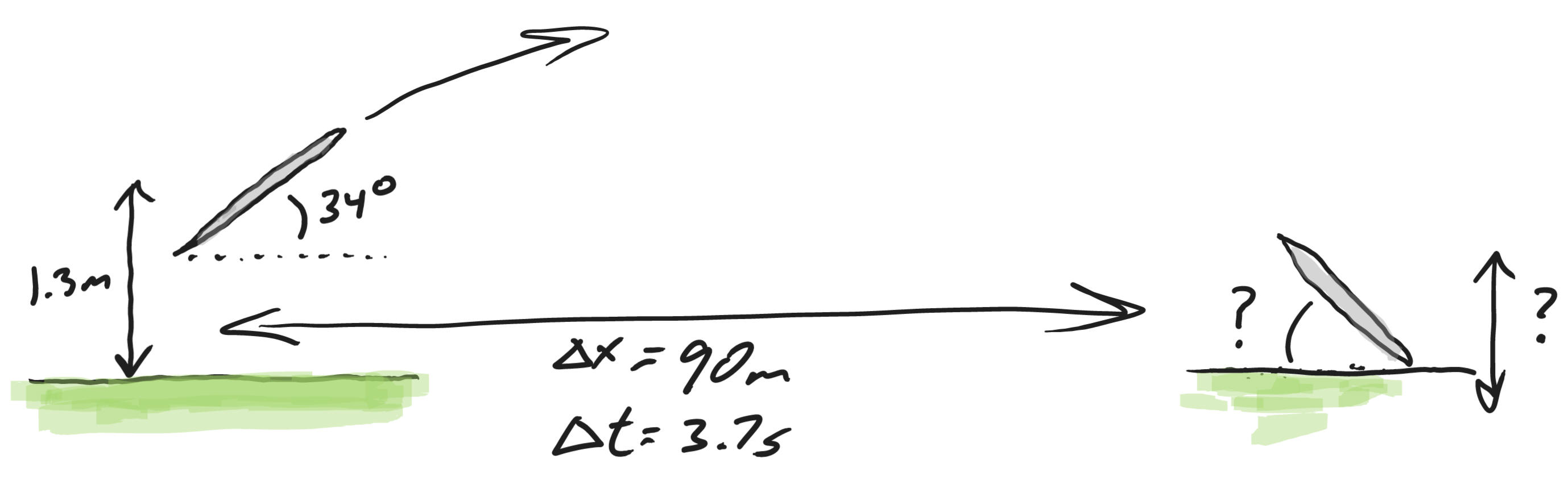
An olympic athlete throws a javelin at an angle of 34 degrees, with respect to the ground. The release point of the javelin is 1.3m above the ground. The javelin travels a horizontal distance of 90 meters and lands after a flight lasting 3.7 seconds.
1. At what angle is the javelin sticking out of the ground at its point of impact? [We will just do this one, but you might want to try #2 on your own. Solutions are below.]
2. It turns out that the field is not level. How much higher or lower is the field at the point of impact, compared to the field at the point of release?
Today:
- Check/review homework
- Finish the projectile challenge. First confirm your setting for the proper speed (it may have changed or you may have a different setup).
- Mr. Pennington's test on pages 12-14: Multiple choice #15-19 and Problems #1-3
- Unit 2 Packet (PDF) Unit 2 Answer Key
Warm Up: If you want to launch a projectile horizontally, from a height of 0.3m, and you want its initial speed to be 4m/s, you should adjust your launcher strength until it travels a horizontal distance of ___?___m.
Today:
- Check/review homework
- Finish the notes on p.6-7 of the handout Unit 2 Answer Key Video of Notes from a past year's Class
- Mini-projectile contest. Calibrate a launcher. Then use your calibration to hit a target
Homework: Unit 2 Answer Key
- #4 on page 9
- Mr. Pennington's multiple choice on pages 10 and 11.
 Class 10.5:
Monday,
9/23/24
Class 10.5:
Monday,
9/23/24Warm Up: Video of this warm-up -- drawing Vx, Vy, and V during projectile motion
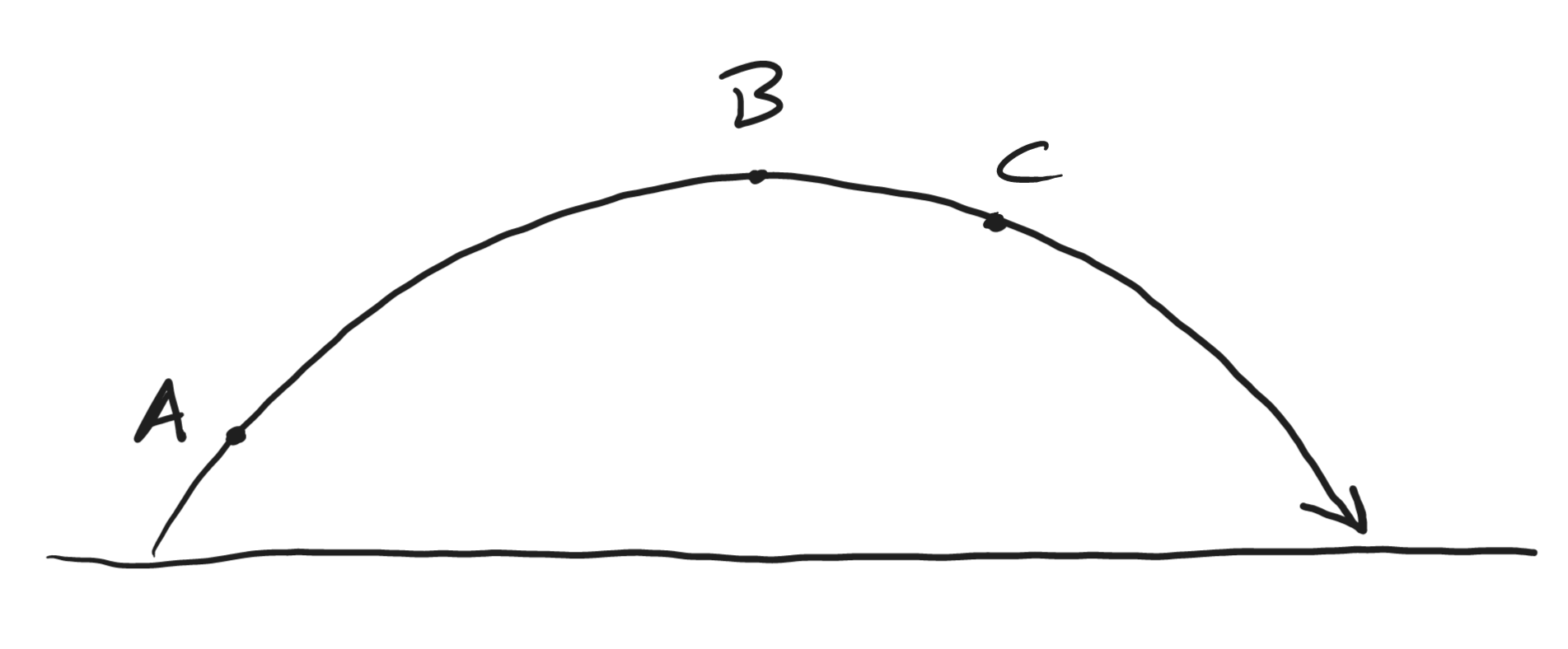
The diagram on the right shows the symmetric trajectory of a free-falling projectile. Sketch the diagram.
1. What does free-falling mean?
2. At each labeled point (A, B, and D) show/label the projectile's overall velocity vector (v), x velocity vector (vx), and y velocity vector (vy).
Today:
- Return retakes -- but some students haven't done the retake, so give them back to me for a while.
- Check/review homework
- Work time
Homework:
Warm Up: None (so there's time for the retake)
Today:
- Optional test retake
- Work time for those not taking the test -- start on the homework, below.
Homework: See class #9.5, below.
 Class
9.5: Thursday,
9/19/24
Class
9.5: Thursday,
9/19/24Warm Up: Here are a couple of 2-D motion simulations...
What's the ideal angle for launching a projectile, if you want it to travel the greatest horizontal distance? Why is that angle best?
Today:
- Check/review homework
- Note the unit conversion from m/s to mph on p. 7. I will expect you to memorize this (1m/s = 2.24mph).
- Unit 2 Packet (PDF)
- Notes -- Introduction to Projectile Problems. Do a practice problem similar to #2 on page 8 (PDF). Video from class
Homework:
- Nothing is due tomorrow. All of this is due on Monday.
- #1 and #2 on page 8.
- #1 and #2 on pages 17 and 18.
- Unit 2 Answer Key
 Class
9: Wednesday,
9/18/24
Class
9: Wednesday,
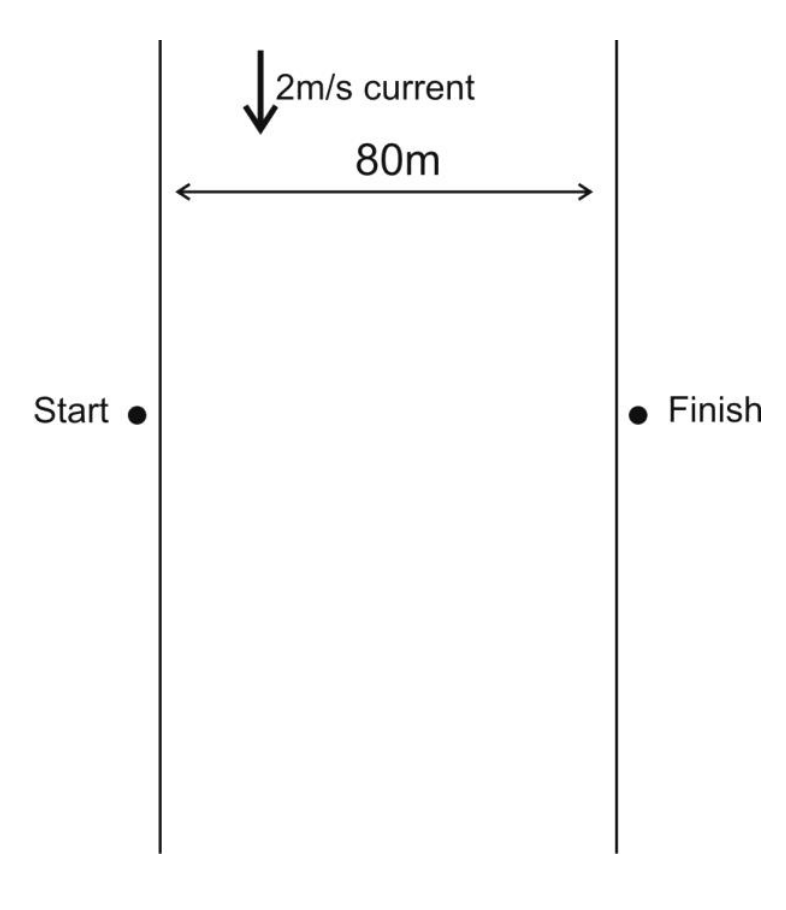
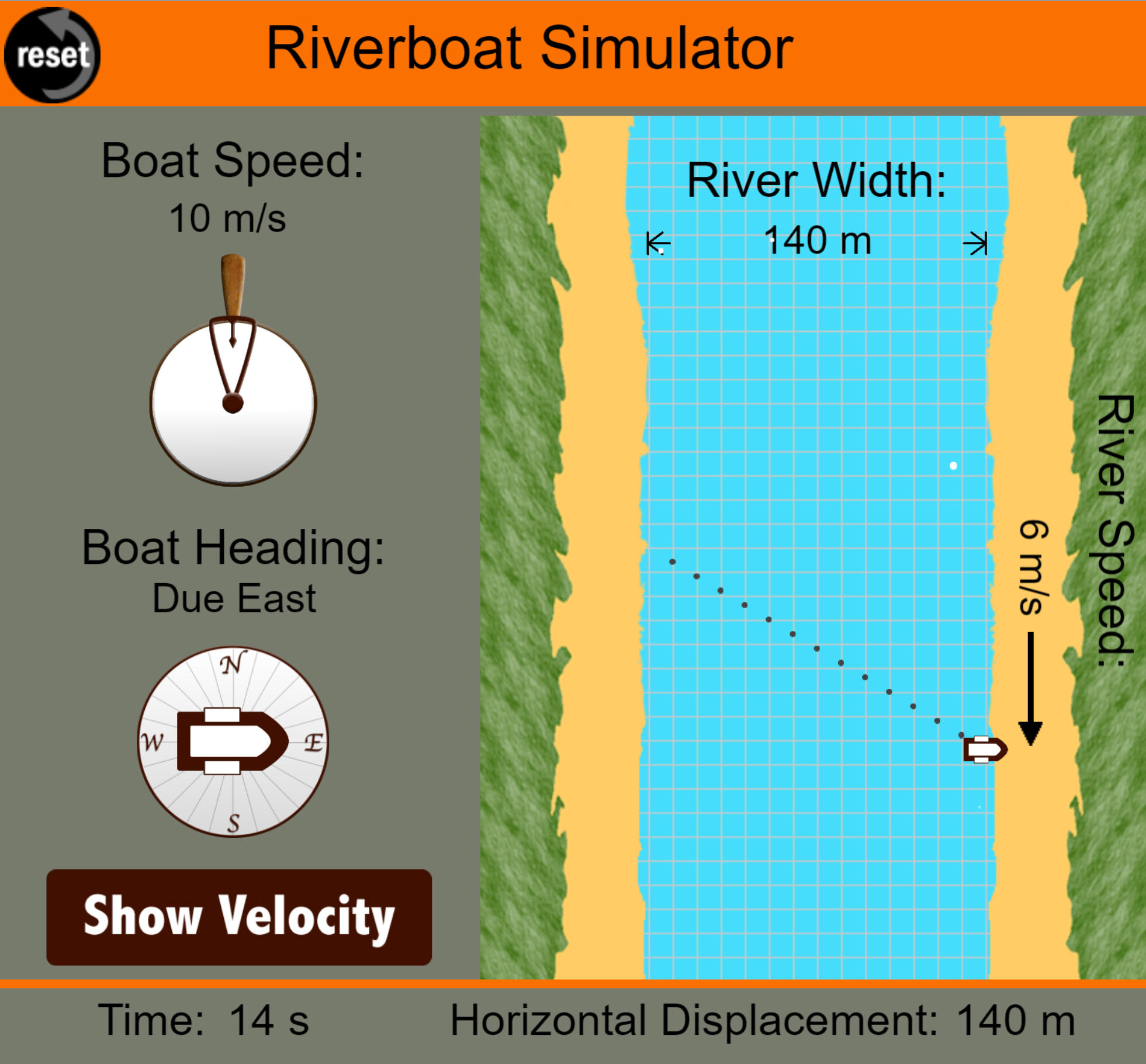
9/18/24Warm Up: Let's explore the "classic river problem" using some helpful tables (vector addition and kinematics)! Here's a review of the problem...
An 80m wide river flows due south at a rate of 2m/s. Jane and Bob are on the west bank of the river, and they want to travel to a point on the opposite bank, directly eastward from their starting point. In still water, Jane and Bob can paddle a canoe at a speed of 3m/s. On land, each of them can travel at a rate of 4m/s...
-
Jane's plan is to adjust her heading so that she travels directly eastward across the the river, in a straight line to the destination.
-
Bob's plan is to head due east and accept the fact that the current will carry him downstream. When he gets to the opposite bank he will travel on land back upstream to the destination.
Whose plan will get them there fastest?
Video of the solution to the warm-up.
Today:
- Check/review homework
- If you're planning to retake the test on Friday, don't forget that review videos are available -- and that you can see me during FLEX -- and that you can email with questions.
- I have added 4 new videos to the "Unit 1 Test: Videos..." material in Google Classroom. These are general help with topics that people struggled with on page 2 and 4 of the test.
- Unit 2 Packet (PDF) Unit 2 Answer Key
- Today's Lesson -- Solve an non-orthogonal river problem -- #4 on p. 5. Video of solution from class -- at the very end, someone gives me the wrong angle for the inverse tangent of 61/71. It should be 40.7 degrees, not 49.3 (the complement of 40.7).
Homework:
- Page 5, #5 and #6.
- Unit 2 Answer Key
Warm Up:
Sketch a head-to-tail diagram for each of the following. Two "component" vectors should add up to the "resultant." The trickiest part is identifying the resultant. [A couple of methods: the resultant is... the dependent variable or the velocity of the "protagonist" relative to the Earth.]
2. A river's 3mph current flows in a direction 15
degrees West of North. A swimmer, whose speed in s till
water is 2m/s, swims across the river with a heading 35 degrees South of
West. What is the swimmer's velocity, relative to the Earth?
till
water is 2m/s, swims across the river with a heading 35 degrees South of
West. What is the swimmer's velocity, relative to the Earth?
3. A superhero steward on an airplane is traveling in a direction 10 degrees East of South, and their speed is 580mph. The plane's velocity is 460mph in a direction 5 degrees West of South. What is the steward's heading and their "speed on a still plane?"
Sketches and answers: --- I got rid of number 1. Just ignore solution #1.
Today:
- Check/review homework
- Sign up for FLEX or email me if you need help preparing for Friday's test retake.
- A1/2 -- I figured out how my spreadsheet worked -- Spreadsheet Solution
- How to solve "river problems." Do an example orthogonal problem. Video from Today's class.
Homework:
- Complete #2 amd 3 -- Change the river's current to 2.5m/s on p. 5. Unit 2 Answer Key
 Class
8: Monday,
9/16/24
Class
8: Monday,
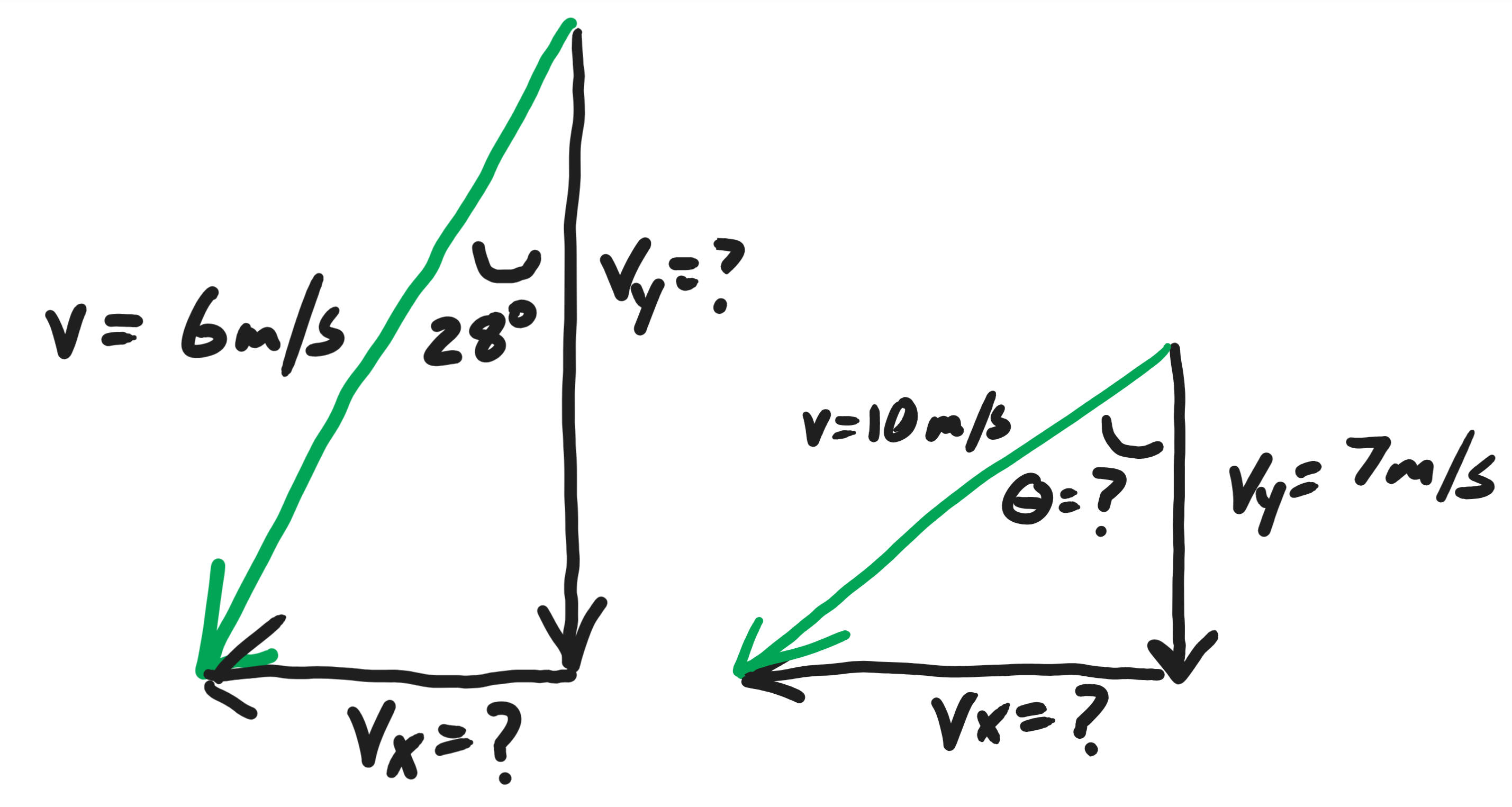
9/16/24Warm Up:
1. Find the missing values of Vx, Vy, and theta.
2. In the diagram on the right, should Vy be -7m/s, instead of 7m/s?
Today:
- In case you're curious... Mathematical (spreadsheet) model of the pendulum warmup from class #6
- Another look at the bonus problem. Spreadsheet Solution
- Notes and Practice:
- Before we really begin... Shoot-n-drop video
- U Unit 2 Packet (PDF) , p. 1-3. Unit 2 Answer Key (practice test in back needs to be updated) Video of Notes
- If we have time
- look at the online textbook Course expectations
- My slideshow?
Homework:
- Finish the rest of the vector addition problems on page 3 of the packet. Unit 2 Answer Key
- For a fun, optional challenge: try the Classic River Problem (p. 4). Don't look at the answer!
Warm Up:
1. Suppose the two vectors (arrows) on the right represent two forces acting on the clam. In what direction will the clam accelerate? How will that acceleration compare to the accelerations we would observe if each force were acting alone?
2. The diagram on the right shows a top view of a train car that is moving at a rate of 2m/s. You are in the car. In which direction and how fast should you walk in order to have the intended velocity shown on the right.
Today:
- Return tests. Check for grading errors.
- Brief intro to vectors and trigonometry -- do some practice
problems with the various functions and inverse functions (make a
video). Here are some example problems...

Homework:
- None to turn in.
- Optional:
- Trig Practice: your trigonometry knowledge is rusty or nonexistent, self-teach about using SohCahToa and inverse functions. You should be able to find plenty of resources with an online search.
- Prepare for the optional retake (next Friday, in class). Watch the relevant provided videos in Google Classroom ("Unit 1 Test: Videos to prepare for the retake"). Sign up for my Flex if you want more help.




 Class
5:
Class
5:  Class
4.5:
Class
4.5: 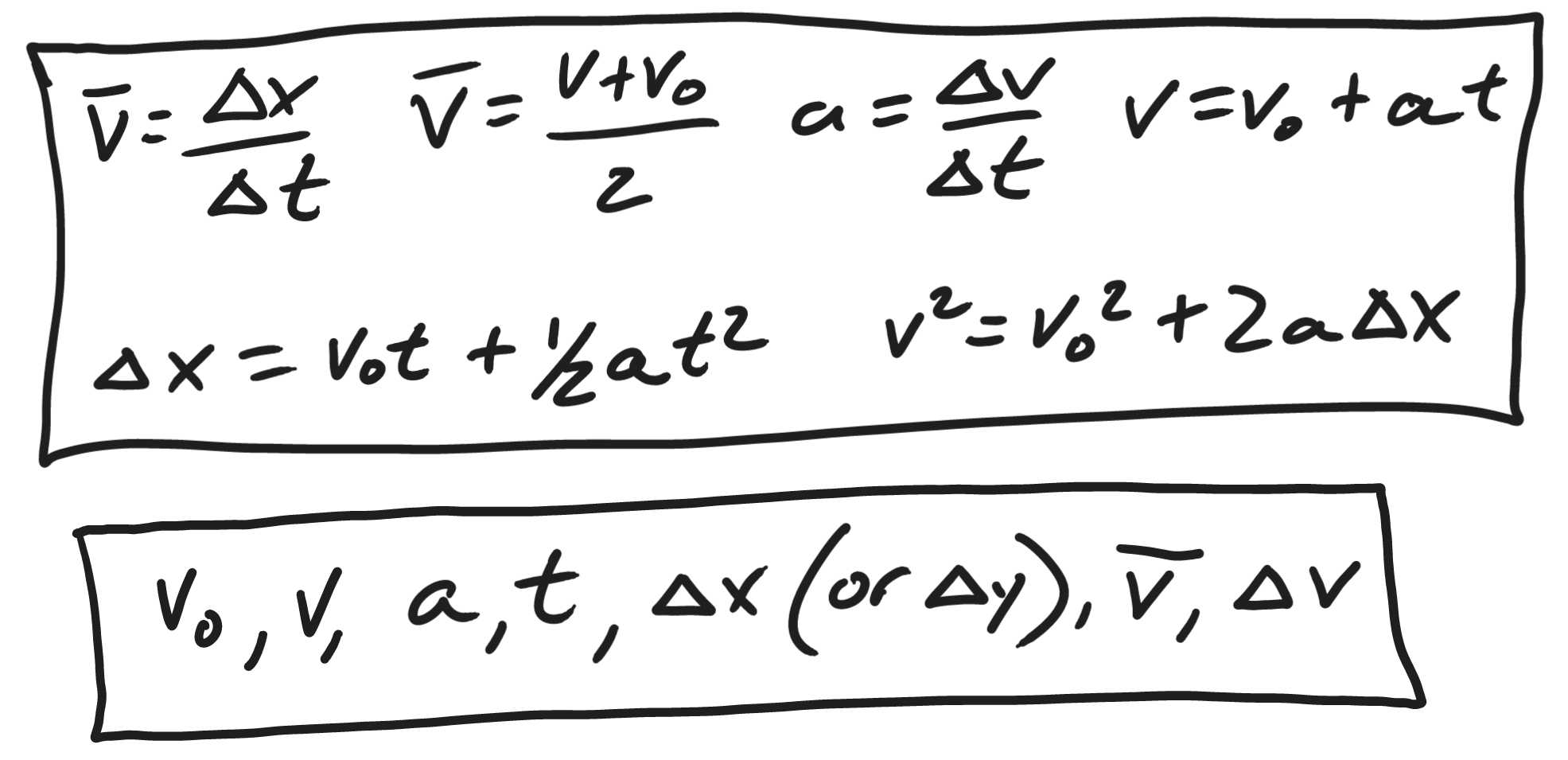 Class
4:
Class
4:  Class
3.5:
Class
3.5: 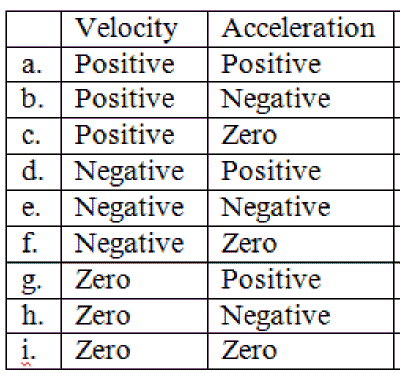 Class
3:
Class
3: 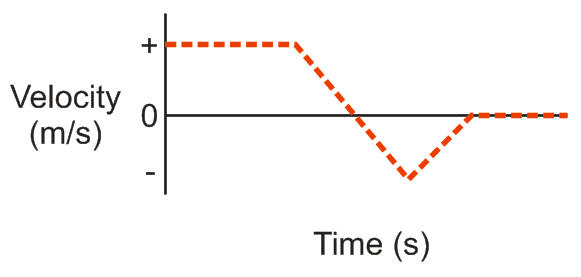 Class
2:
Class
2:  Class 1.5:
Class 1.5:
 Spin
one of the "sprotating cylinders" by pressing one end until it squirts
out from under your finger. Try pressing the other end.
Spin
one of the "sprotating cylinders" by pressing one end until it squirts
out from under your finger. Try pressing the other end.